[四川]2011---2012学年四川省成都铁中高二10月考数学试卷
下列说法法正确的是 ( )
| A.三点确定一个平面 | B.四边形一定是平面图形 |
| C.梯形一定是平面图形 | D.平面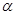 和平面 和平面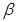 有不同在一条直线上的三个交点 有不同在一条直线上的三个交点 |
下列四个正方体图形中, 、
、 为正方体的两个顶点,
为正方体的两个顶点, 、
、 、
、 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出 ∥平面
∥平面 的图形的序号是( )
的图形的序号是( )
| A.①③ | B.①④ | C.②③  |
D.②④ |
已知球心到过球面上 ,
, ,
, 三点的截面的距离等于球半径的一半,且
三点的截面的距离等于球半径的一半,且 ,则球面面积是( )
,则球面面积是( )
A. |
B. |
C. |
D. |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. |
B. |
C. |
D. |
设m、n是两条不同的直线, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ,
, ,则
,则 ②若
②若 ∥
∥ ,
, ∥
∥ ,
, ,则
,则
③若 ,
, ,则
,则 ④若
④若 则
则 ∥
∥
其中正确命题的序号是 ( )
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
正四棱柱 (底面是正方形,侧棱垂直底面的四棱柱)中,
(底面是正方形,侧棱垂直底面的四棱柱)中, ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )
A. |
B. |
C. |
D. |
如图,三棱柱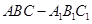 中,侧棱
中,侧棱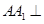 底面
底面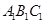 ,底面三角形
,底面三角形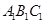 是正三角形,
是正三角形,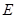 是
是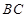 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A.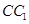 与 与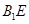 是异面直线 是异面直线 |
B.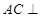 平面 平面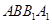 |
C.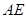 , ,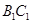 为异面直线,且 为异面直线,且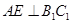 |
D.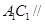 平面 平面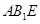 |

如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )
| A.4 | B.5 | C.6 | D.7 |
圆心为 的圆与直线
的圆与直线 交于
交于 、
、 两点,
两点, 为坐标原点,且满足
为坐标原点,且满足 ,则圆
,则圆 的方程为( )
的方程为( )
A. |
B. |
C. |
D. |
在平面几何中,有如下结论:三边相等的三角形内任意一点到三角形三边的距离之和为定值。拓展到空间,类比平面几何的上述结论,可得:四个面均为等边三角形的四面体内任意一点_________________________________
将边长为1的正方体木块 沿平面
沿平面 锯开后得到两个三棱柱,那么由这两个三棱柱组成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)
锯开后得到两个三棱柱,那么由这两个三棱柱组成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)
已知直线 经过直线
经过直线 与直线
与直线 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
.
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ)求直线 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积
如图:在三棱锥 中,已知点
中,已知点 、
、 、
、 分别为棱
分别为棱 、
、 、
、 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)若 ,
, ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
求证:平面A B1D1∥平面EFG;
求二面角 的正切值。
的正切值。
如图:已知平面 //平面
//平面 ,点A、B在平面
,点A、B在平面 内,点C、D在
内,点C、D在 内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
求证:(Ⅰ)E、F、G、H四点共面;
(Ⅱ)平面EFGH//平面 .
.
如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是 的中点.
的中点.
(I)求证: ;
;
(Ⅱ)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
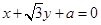 (
(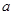 为实常数)的倾斜角的大小是( )
为实常数)的倾斜角的大小是( )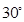
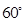
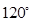
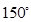

 ,点
,点 在直线
在直线 上,若直线
上,若直线 垂直于直线
垂直于直线 , 则点
, 则点



 ,表示的平面区域的面积是
,表示的平面区域的面积是 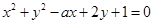 关于直线
关于直线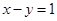 对称的圆的方程是
对称的圆的方程是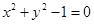 ,则实数
,则实数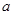 的值是
的值是  及圆
及圆 :
: .
. 过点
过点 且与圆心
且与圆心 与圆
与圆 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程; 与圆
与圆 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号