如图,设椭圆
(1)求直线 被椭圆截得到的弦长(用a,k表示)
(2)若任意以点 为圆心的圆与椭圆至多有三个公共点,求椭圆的离心率的取值范围.
已知 ,函数 ,其中
(1)求使得等式 成立的x的取值范围
(2)(1)求 的最小值
(3)求 在 上的最大值
如图,在三棱台 中,已知平面 平面 , , , , ,
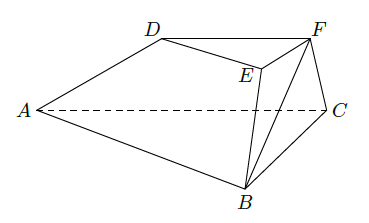
(1)求证: 平面 ;
(2)求二面角 的余弦值.
在 中,内角A,B,C所对的边分别为a,b,c,已知 .
(1)证明:
(2)若 的面积 ,求角A的大小.
已知函数 .
(1)求曲线 在点 处的切线方程;
(2)求函数 在区间 上的最大值和最小值.
已知抛物线 过点 .过点 作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
为了研究一种新药的疗效,选100名患者随机分成两组,每组各 名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标 和 的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.
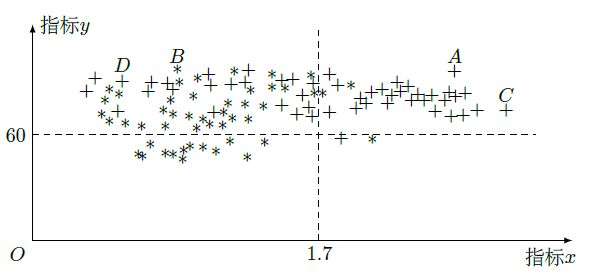
(1)从服药的50名患者中随机选出一人,求此人指标 的值小于 的概率;
(2)从图中A,B,C,D四人中随机选出两人,记 为选出的两人中指标x的值大于1.7的人数,求 的分布列和数学期望 ;
(3)试判断这100名患者中服药者指标 数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
如图,在四棱锥 中,底面 为正方形,平面 平面 ,点M在线段PB上, 平面 , , .
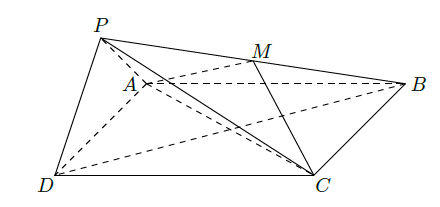
(1)求证:M为PB的中点;
(2)求二面角 的大小;
(3)求直线MC与平面BDP所成角的正弦值.
设常数 ,在平面直角坐标系xOy中,已知点F(2,0),直线 : ,曲线 : , 与x轴交于点A,与 交于点B,P、Q分别是曲线 与线段AB上的动点。
(1)用t表示点B到点F的距离;
(2)设t=3, ,线段OQ的中点在直线FP上,求△AQP的面积;
(3)设t=8,是否存在以FP、FQ为邻边的矩形FPEQ,使得点E在 上?若存在,求点P的坐标;若不存在,说明理由。
某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时,某地上班族S中的成员仅以自驾或公交方式通勤,分析显示:当S中 的成员自驾时,自驾群体的人均通勤时间为
(单位:分钟),
而公交群体的人均通勤时间不受x影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当x在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族S的人均通勤时间 的表达式;讨论 的单调性,并说明其实际意义。
设常数 ,函数
(1)若 为偶函数,求 的值;
(2)若 ,求方程 在区间 上的解。
已知圆锥的顶点为 ,底面圆心为 ,半径为 。
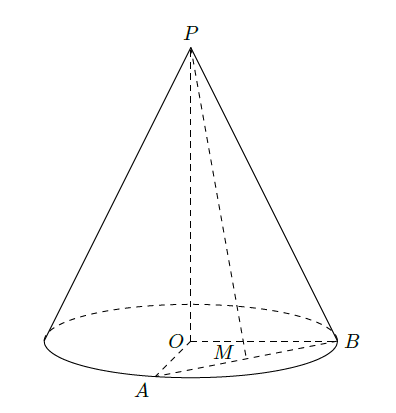
(1)设圆锥的母线长为4,求圆锥的体积;
(2)设 , 是底面半径,且 ,M为线段AB的中点,如图,求异面直线PM与OB所成的角的大小.
在平面直角坐标系 中,点P到点F 的距离的4倍与它到直线 的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标与18之和
(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线I与轨迹C相交于M,N两点,求线段MN长度的最大值。