在三棱锥 A- BCD中,已知 CB= CD= , BD=2, O为 BD的中点, AO⊥平面 BCD, AO=2, E为 AC的中点.
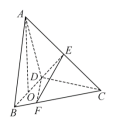
(1)求直线 AB与 DE所成角的余弦值;
(2)若点 F在 BC上,满足 BF= BC,设二面角 F- DE- C的大小为 θ,求sin θ的值.
在平面直角坐标系 xOy中,已知椭圆 的左、右焦点分别为 F 1, F 2,点 A在椭圆 E上且在第一象限内, AF 2⊥ F 1 F 2,直线 AF 1与椭圆 E相交于另一点 B.
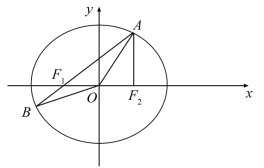
(1)求△ AF 1 F 2的周长;
(2)在 x轴上任取一点 P,直线 AP与椭圆 E的右准线相交于点 Q,求 的最小值;
(3)设点 M在椭圆 E上,记△ OAB与△ MAB的面积分别为 S 1, S 2,若 S 2=3 S 1,求点 M的坐标.
某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底 O在水平线 MN上、桥 AB与 MN平行, 为铅垂线( 在 AB上).经测量,左侧曲线 AO上任一点 D到 MN的距离 (米)与 D到 的距离 a(米)之间满足关系式 ;右侧曲线 BO上任一点 F到 MN的距离 (米)与 F到 的距离 b(米)之间满足关系式 .已知点 B到 的距离为40米.
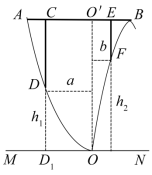
(1)求桥 AB的长度;
(2)计划在谷底两侧建造平行于 的桥墩 CD和 EF,且 CE为80米,其中 C, E在 AB上(不包括端点).桥墩 EF每米造价 k(万元)、桥墩 CD每米造价 (万元)( k>0).问 为多少米时,桥墩 CD与 EF的总造价最低?
在△ ABC中,角 A, B, C的对边分别为 a, b, c,已知 .
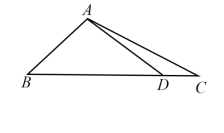
(1)求 的值;
(2)在边 BC上取一点 D,使得 ,求 的值.
在三棱柱 ABC- A 1 B 1 C 1中, AB⊥ AC, B 1 C⊥平面 ABC, E, F分别是 AC, B 1 C的中点.

(1)求证: EF∥平面 AB 1 C 1;
(2)求证:平面 AB 1 C⊥平面 ABB 1.
已知 为等差数列, 为等比数列, .
(Ⅰ)求 和 的通项公式;
(Ⅱ)记 的前 项和为 ,求证: ;
(Ⅲ)对任意的正整数 ,设 求数列 的前 项和.
已知椭圆 的一个顶点为 ,右焦点为 ,且 ,其中 为原点.
(Ⅰ)求椭圆 方程;
方程;
(Ⅱ)已知点 满足 ,点 在椭圆上( 异于椭圆的顶点),直线 与以 为圆心的圆相切于点 ,且 为线段 的中点.求直线 的方程.
如图,在三棱柱 中, 平面 , ,点 分别在棱 和棱 上,且 为棱 的中点.

(Ⅰ)求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)求直线 与平面 所成角的正弦值.
在
中,角 所对的边分别为
.已知
.
所对的边分别为
.已知
.
(Ⅰ)求角 的大小;
(Ⅱ)求 的值;
(Ⅲ)求 的值.
如图,已知椭圆 ,抛物线 ,点 A是椭圆 与抛物线 的交点,过点 A的直线 l交椭圆 于点 B,交抛物线 于 M( B, M不同于 A).

(Ⅰ)若 ,求抛物线 的焦点坐标;
(Ⅱ)若存在不过原点的直线 l使 M为线段 AB的中点,求 p的最大值.
已知数列{an},{bn},{cn}中, .
(Ⅰ)若数列{bn}为等比数列,且公比 ,且 ,求q与an的通项公式;
(Ⅱ)若数列{bn}为等差数列,且公差 ,证明: .
如图,三棱台 DEF- ABC中,面 ADFC⊥面 ABC,∠ ACB=∠ ACD=45°, DC=2 BC.

(I)证明: EF⊥ DB;
(II)求 DF与面 DBC所成角的正弦值.
在锐角△ ABC中,角 A, B, C的对边分别为 a, b, c,且 .
(I)求角 B;
(II)求cos A+cos B+cos C的取值范围.
已知椭圆 过点 ,且 .
(Ⅰ)求椭圆C的方程:
(Ⅱ)过点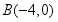 的直线l交椭圆C于点
,直线
分别交直线
于点
.求
的值.
的直线l交椭圆C于点
,直线
分别交直线
于点
.求
的值.