设 ,
, ,Q=
,Q= ;若将
;若将 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列 的前三项.
的前三项.
(1)试比较M、P、Q的大小;
(2)求 的值及
的值及 的通项;
的通项;
(3)记函数 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为 ,
,
设
 ,求
,求 ,并证明
,并证明 .
.
已知数列 是首项为1,公差为
是首项为1,公差为 的等差数列,数列
的等差数列,数列 是首项为1,公比为
是首项为1,公比为 的等比
的等比
数列.
(1)若 ,
, ,求数列
,求数列 的前
的前 项和;
项和;
(2)若存在正整数 ,使得
,使得 .试比较
.试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
(本小题满分14分)已知数列{an}是以d为公差的等差数列,数列{bn}是以q为公比的等比数列
(Ⅰ)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3<5b2+a88-180,求整数q的值
(Ⅱ)在(Ⅰ)的条件下,试问数列{bn}中是否存在一项bk,使得b,k恰好可以表示为该数列中连续P(P∈N,P≥2)项和?请说明理由。
(Ⅲ)若b1=ar,b2=as≠ar, b3=at(其中t>s>r,且(s—r)是(t—r)的约数)求证:数列{bn}中每一项都是数列{an}中的项.
在等差数列 中,已知 ,则 ()
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
定义数列 :
: ,且对任意正整数
,且对任意正整数 ,有
,有 .
.
(1)求数列 的通项公式与前
的通项公式与前 项和
项和 ;
;
(2)问是否存在正整数 ,使得
,使得 ?若存在,则求出所有的正整数对
?若存在,则求出所有的正整数对 ;若不存在,则加以证明.
;若不存在,则加以证明.
(本小题满分16分)已知数列 ,
, 满足
满足 ,其中
,其中 .(Ⅰ)若
.(Ⅰ)若 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,且
,且 .
.
(ⅰ)记 ,求证:数列
,求证:数列 为等差数列;
为等差数列;
(ⅱ)若数列 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项 应满足的条件.
应满足的条件.
已知数列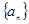 中,
中,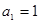 ,
, 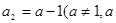 为实常数),前
为实常数),前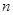 项和
项和 恒为正值,且当
恒为正值,且当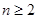 时,
时,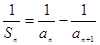 .
.
⑴求证:数列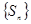 是等比数列;
是等比数列;
⑵设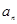 与
与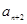 的等差中项为
的等差中项为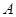 ,比较
,比较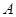 与
与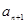 的大小;
的大小;
⑶设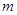 是给定的正整数,
是给定的正整数, .现按如下方法构造项数为
.现按如下方法构造项数为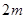 有穷数列
有穷数列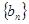 :
:
当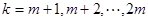 时,
时,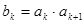 ;
;
当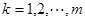 时,
时, .
.
求数列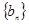 的前
的前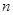 项和
项和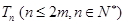 .
.
(本小题满分14分)已知数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上;数列
上;数列 满足
满足 ,且
,且 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求使不等式
,求使不等式 对一切
对一切 都成立的最大正整数
都成立的最大正整数 的值;
的值;
(3)设 ,是否存在
,是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本题满分14分)
已知正项数列 满足:对任意正整数
满足:对任意正整数 ,都有
,都有 成等差数列,
成等差数列, 成等比数列,且
成等比数列,且
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ) 设 如果对任意正整数
如果对任意正整数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知点Pn(an,bn)都在直线L:y=2x+2上,P1为直线L与x轴的交点,数
列{an}成等差数列,公差为1(n∈N*)。
(I)求数列{an},{bn}的通项公式;
(II)求证: (n≥3,n∈N*)。
(n≥3,n∈N*)。
 证明以下命题:
证明以下命题:
(Ⅰ)对任一正整a,都存在整数b,c(b<c),使得 成等差数列。
成等差数列。
(Ⅱ)存在无穷多个互不相似的三角形△ ,其边长
,其边长 为正整数且
为正整数且 成等差数列。
成等差数列。