已知点Pn(an，bn)都在直线L：y=2x+2上，P1为直线L与x轴的交点，数
列{an}成等差数列，公差为1(n∈N＊)。
（I）求数列{an}，{bn}的通项公式；
（II）求证：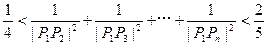
(n≥3，n∈N＊)。
相关试题
是数列
的前
项和，
．
的通项；
，求数列
的前
．
为菱形，且
，
．
；
，求二面角
的余弦值。
．
，且
，求θ的值；
，且△ABC的面积为
，求sinA＋sinB的值．
满足
，且对任意
，都有
．
对任意
恒成立，求实数k的取值范围．相关知识点
推荐套卷
已知点Pn(an，bn)都在直线L：y=2x+2上，P1为直线L与x轴的交点，数
列{an}成等差数列，公差为1(n∈N＊)。
（I）求数列{an}，{bn}的通项公式；
（II）求证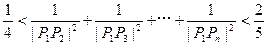：(n≥3，n∈N＊)。
粤公网安备 44130202000953号