已知数列 满足:
满足: 是数列
是数列 的前n项和.数列
的前n项和.数列 前n项的积为
前n项的积为 ,且
,且
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)是否存在常数a,使得 成等差数列?若存在,求出a,若不存在,说明理由;
成等差数列?若存在,求出a,若不存在,说明理由;
(Ⅲ)是否存在 ,满足对任意自然数
,满足对任意自然数 时,
时, 恒成立,若存在,求出m的值;若不存在,说明理由.
恒成立,若存在,求出m的值;若不存在,说明理由.
已知等差数列 的首项
的首项 ,
, ,前
,前 项和为
项和为 .
.
(I)求 及
及 ;
;
(Ⅱ)设 ,
, ,求
,求 的最大值.
的最大值.
设等比数列 的首项为
的首项为 ,公比为
,公比为 (
( 为正整数),且满足
为正整数),且满足 是
是 与
与 的等差中项;数列
的等差中项;数列 满足
满足 (
( ).
).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)试确定 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(Ⅲ)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数 ,在
,在 与
与 之间插入
之间插入 个2,得到一个新数列
个2,得到一个新数列 . 设
. 设 是数列
是数列 的前
的前 项和,试求满足
项和,试求满足 的所有正整数
的所有正整数 .
.
已知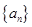 为等差数列,且
为等差数列,且 .
.
(Ⅰ)求数列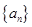 的通项公式及其前
的通项公式及其前 项和
项和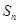 ;
;
(Ⅱ)若数列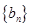 满足
满足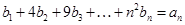 求数列
求数列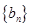 的通项公式.
的通项公式.
设 是首项为
是首项为 ,公差为
,公差为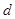 的等差数列
的等差数列 ,
,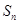 是其前
是其前 项和.
项和.
(1)若 ,
,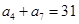 ,求数列
,求数列 的通项公式;
的通项公式;
(2)记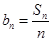 ,
, ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: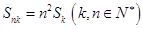 .
.