如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角 ,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )

A. B.
C. D.
数学兴趣小组根据无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为 ,则旗杆的高度约为
米.
(结果精确到1米,参考数据: ,

居家学习期间,小晴同学运用所学知识在自家阳台测对面大楼的高度.如图,她利用自制的测角仪测得该大楼顶部的仰角为 ,底部的俯角为 ;又用绳子测得测角仪距地面的高度 为 .求该大楼的高度(结果精确到 .
(参考数据: , ,

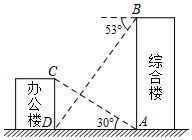
在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部 处测得办公楼底部 处的俯角是 ,从综合楼底部 处测得办公楼顶部 处的仰角恰好是 ,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据 , ,
如图,小明在距离地面30米的 处测得 处的俯角为 , 处的俯角为 .若斜面坡度为 ,则斜坡 的长是 米.

如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道 .无人机从点 的正上方点 ,沿正东方向以 的速度飞行 到达点 ,测得 的俯角为 ,然后以同样的速度沿正东方向又飞行 到达点 ,测得点 的俯角为 .
(1)求无人机的高度 (结果保留根号);
(2)求 的长度(结果精确到 .
(参考数据: , , ,

如图,无人机在离地面60米的 处,观测楼房顶部 的俯角为 ,观测楼房底部 的俯角为 ,求楼房的高度.

如图,为了测量"四川大渡河峡谷"石碑的高度,佳佳在点 处测得石碑顶 点的仰角为 ,她朝石碑前行5米到达点 处,又测得石碑顶 点的仰角为 ,那么石碑的高度 的长 米.(结果保留根号)

如图,山顶上有一个信号塔 ,已知信号塔高 米,在山脚下点 处测得塔底 的仰角 ,塔顶 的仰角 ,求山高 (点 , , 在同一条竖直线上).
(参考数据: , , .

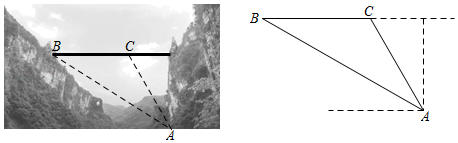
张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面 , 的仰角分别为 , ,测得 长为320米,求观测点 到桥面 的距离.(结果保留整数,参考数据:
如图,楼顶上有一个广告牌 ,从与楼 相距 的 处观测广告牌顶部 的仰角为 ,观测广告牌底部 的仰角为 ,求广告牌 的高度.(结果保留小数点后一位,参考数据: , , , ,

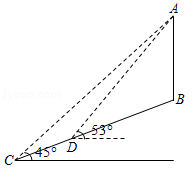
资阳市为实现 网络全覆盖, 年拟建设 基站七千个.如图,在坡度为 的斜坡 上有一建成的基站塔 ,小芮在坡脚 测得塔顶 的仰角为 ,然后她沿坡面 行走13米到达 处,在 处测得塔顶 的仰角为 .(点 、 、 、 均在同一平面内)(参考数据: , ,
(1)求 处的竖直高度;
(2)求基站塔 的高.
如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度 点处时,无人机测得操控者 的俯角为 ,测得小区楼房 顶端点 处的俯角为 .已知操控者 和小区楼房 之间的距离为45米,小区楼房 的高度为 米.
(1)求此时无人机的高度;
(2)在(1)条件下,若无人机保持现有高度沿平行于 的方向,并以5米 秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点 , , , 都在同一平面内.参考数据: , .计算结果保留根号)

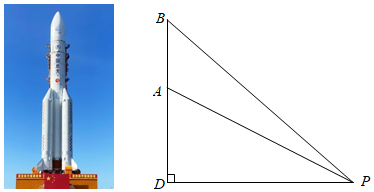
我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点 处时,在 处测得 点的仰角 为 且 与 两点的距离为6千米,它沿铅垂线上升7.5秒后到达 处,此时在 处测得 点的仰角 为 ,求天舟二号从 处到 处的平均速度.(结果精确到 ,取 ,