位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
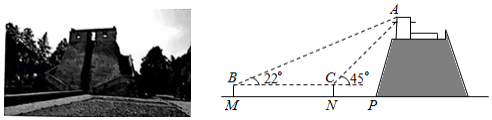
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道 上架设测角仪,先在点 处测得观星台最高点 的仰角为 ,然后沿 方向前进 到达点 处,测得点 的仰角为 .测角仪的高度为 .
(1)求观星台最高点 距离地面的高度(结果精确到 .参考数据: , , , ;
(2)“景点简介”显示,观星台的高度为 .请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
相关知识点
推荐套卷
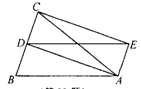
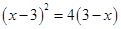
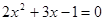
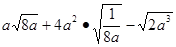 (a>0)
(a>0) 粤公网安备 44130202000953号
粤公网安备 44130202000953号