如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上1、2、3、4四个数字;转盘B被均匀分成6等份,每份标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下:
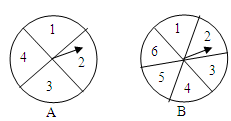
(1)同时转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),用所指的两个数字作乘积,如果所得的积是偶数,那么甲胜;如果所得的积是奇数,那么乙胜.
你认为这样的规则是否公平?请你说明理由;如果不公平,请你设计一个公平的规则,并说明理由.