初中数学相似三角形的判定与性质解答题

定义：有三个内角相等的四边形叫三等角四边形．

（1）三等角四边形 $\mathit{ABCD}$中， $\angle A=\angle B=\angle C$，求 $\angle A$的取值范围；

（2）如图，折叠平行四边形纸片 $\mathit{DEBF}$，使顶点 $E$， $F$分别落在边 $\mathit{BE}$， $\mathit{BF}$上的点 $A$， $C$处，折痕分别为 $\mathit{DG}$， $\mathit{DH}$．求证：四边形 $\mathit{ABCD}$是三等角四边形．

（3）三等角四边形 $\mathit{ABCD}$中， $\angle A=\angle B=\angle C$，若 $\mathit{CB}=\mathit{CD}=4$，则当 $\mathit{AD}$的长为何值时， $\mathit{AB}$的长最大，其最大值是多少？并求此时对角线 $\mathit{AC}$的长．

已知：在 $\mathit{\Delta ABC}$外分别以 $\mathit{AB}$， $\mathit{AC}$为边作 $\mathit{\Delta AEB}$与 $\mathit{\Delta AFC}$．

（1）如图1， $\mathit{\Delta AEB}$与 $\mathit{\Delta AFC}$分别是以 $\mathit{AB}$， $\mathit{AC}$为斜边的等腰直角三角形，连接 $\mathit{EF}$．以 $\mathit{EF}$为直角边构造 $\text{Rt}\Delta \text{EFG}$，且 $\mathit{EF}=\mathit{FG}$，连接 $\mathit{BG}$， $\mathit{CG}$， $\mathit{EC}$．

求证：① $\mathit{\Delta AEF}\cong \mathit{\Delta CGF}$．

②四边形 $\mathit{BGCE}$是平行四边形．

（2）小明受到图1的启发做了进一步探究：

如图2，在 $\mathit{\Delta ABC}$外分别以 $\mathit{AB}$， $\mathit{AC}$为斜边作 $\text{Rt}\Delta \text{AEB}$与 $\text{Rt}\Delta \text{AFC}$，并使 $\angle \mathit{FAC}=\angle \mathit{EAB}=30°$，取 $\mathit{BC}$的中点 $D$，连接 $\mathit{DE}$， $\mathit{EF}$后发现，两者间存在一定的数量关系且夹角度数一定，请你帮助小明求出 $\frac{\mathit{ED}}{\mathit{EF}}$的值及 $\angle \mathit{DEF}$的度数．

（3）小颖受到启发也做了探究：

如图3，在 $\mathit{\Delta ABC}$外分别以 $\mathit{AB}$， $\mathit{AC}$为底边作等腰三角形 $\mathit{AEB}$和等腰三角形 $\mathit{AFC}$，并使 $\angle \mathit{CAF}+\angle \mathit{EAB}=90°$，取 $\mathit{BC}$的中点 $D$，连接 $\mathit{DE}$， $\mathit{EF}$后发现，当给定 $\angle \mathit{EAB}=\alpha$时，两者间也存在一定的数量关系且夹角度数一定，若 $\mathit{AE}=m$， $\mathit{AB}=n$，请你帮助小颖用含 $m$， $n$的代数式直接写出 $\frac{\mathit{ED}}{\mathit{EF}}$的值，并用含 $\alpha$的代数式直接表示 $\angle \mathit{DEF}$的度数．

如图，点 $P$为正方形 $\mathit{ABCD}$的对角线 $\mathit{AC}$上的一点，连接 $\mathit{BP}$并延长交 $\mathit{CD}$于点 $E$，交 $\mathit{AD}$的延长线于点 $F$， $\odot O$是 $\mathit{\Delta DEF}$的外接圆，连接 $\mathit{DP}$．

（1）求证： $\mathit{DP}$是 $\odot O$的切线；

（2）若 $\tan \angle \mathit{PDC}=\frac{1}{2}$，正方形 $\mathit{ABCD}$的边长为4，求 $\odot O$的半径和线段 $\mathit{OP}$的长．

如图， $\mathit{AB}$ 是 $\odot O$ 直径，点 $C$ ， $D$ 为 $\odot O$ 上的两点，且 $\stackrel{̂}{\mathit{AD}}=\stackrel{̂}{\mathit{CD}}$ ，连接 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $E$ ， $\odot O$ 的切线 $\mathit{AF}$ 与 $\mathit{BD}$ 延长线相交于点 $F$ ， $A$ 为切点．

（1）求证： $\mathit{AF}=\mathit{AE}$ ；

（2）若 $\mathit{AB}=8$ ， $\mathit{BC}=2$ ，求 $\mathit{AF}$ 的长．

如图， $\mathit{AB}$为 $\odot O$的直径，弦 $\mathit{CD}\perp \mathit{AB}$，垂足为点 $P$，直线 $\mathit{BF}$与 $\mathit{AD}$的延长线交于点 $F$，且 $\angle \mathit{AFB}=\angle \mathit{ABC}$．

（1）求证：直线 $\mathit{BF}$是 $\odot O$的切线．

（2）若 $\mathit{CD}=2\sqrt{3}$， $\mathit{OP}=1$，求线段 $\mathit{BF}$的长．

如图，在平行四边形 $\mathit{ABCD}$ 中， $E$ 为 $\mathit{DC}$ 边的中点，连接 $\mathit{AE}$ ，若 $\mathit{AE}$ 的延长线和 $\mathit{BC}$ 的延长线相交于点 $F$ ．

（1）求证： $\mathit{BC}=\mathit{CF}$ ；

（2）连接 $\mathit{AC}$ 和 $\mathit{BE}$ 相交于点为 $G$ ，若 $\mathit{\Delta GEC}$ 的面积为2，求平行四边形 $\mathit{ABCD}$ 的面积．

从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

（1）如图1，在 $\mathit{\Delta ABC}$中， $\mathit{CD}$为角平分线， $\angle A=40°$， $\angle B=60°$，求证： $\mathit{CD}$为 $\mathit{\Delta ABC}$的完美分割线．

（2）在 $\mathit{\Delta ABC}$中， $\angle A=48°$， $\mathit{CD}$是 $\mathit{\Delta ABC}$的完美分割线，且 $\mathit{\Delta ACD}$为等腰三角形，求 $\angle \mathit{ACB}$的度数．

（3）如图2， $\mathit{\Delta ABC}$中， $\mathit{AC}=2$， $\mathit{BC}=\sqrt{2}$， $\mathit{CD}$是 $\mathit{\Delta ABC}$的完美分割线，且 $\mathit{\Delta ACD}$是以 $\mathit{CD}$为底边的等腰三角形，求完美分割线 $\mathit{CD}$的长．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ACB}=90°$ ，延长 $\mathit{CA}$ 到点 $D$ ，以 $\mathit{AD}$ 为直径作 $\odot O$ ，交 $\mathit{BA}$ 的延长线于点 $E$ ，延长 $\mathit{BC}$ 到点 $F$ ，使 $\mathit{BF}=\mathit{EF}$ ．

（1）求证： $\mathit{EF}$ 是 $\odot O$ 的切线；

（2）若 $\mathit{OC}=9$ ， $\mathit{AC}=4$ ， $\mathit{AE}=8$ ，求 $\mathit{BF}$ 的长．

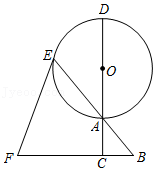
我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”

（1）概念理解：

请你根据上述定义举一个等邻角四边形的例子；

（2）问题探究：

如图1，在等邻角四边形 $\mathit{ABCD}$中， $\angle \mathit{DAB}=\angle \mathit{ABC}$， $\mathit{AD}$， $\mathit{BC}$的中垂线恰好交于 $\mathit{AB}$边上一点 $P$，连接 $\mathit{AC}$， $\mathit{BD}$，试探究 $\mathit{AC}$与 $\mathit{BD}$的数量关系，并说明理由；

（3）应用拓展：

如图2，在 $\text{Rt}\Delta \text{ABC}$与 $\text{Rt}\Delta \text{ABD}$中， $\angle C=\angle D=90°$， $\mathit{BC}=\mathit{BD}=3$， $\mathit{AB}=5$，将 $\text{Rt}\Delta \text{ABD}$绕着点 $A$顺时针旋转角 $\alpha (0°<\angle \alpha <\angle \mathit{BAC})$得到 $\mathit{Rt}$△ $\mathit{AB}\text{'}D\text{'}$（如图 $3)$，当凸四边形 $\mathit{AD}\text{'}\mathit{BC}$为等邻角四边形时，求出它的面积．

如图1，在四边形 $\mathit{ABCD}$中，若 $\mathit{AC}$平分 $\angle \mathit{BAD}$， $A{C}^2=\mathit{AB}·\mathit{AD}$，且 $\mathit{AD}=\mathit{AB}+\mathit{AC}$，则我们称这样的四边形 $\mathit{ABCD}$为“黄金四边形”， $\angle \mathit{BAD}$称为“黄金角”．

【概念理解】（1）已知四边形 $\mathit{ABCD}$为“黄金四边形”， $\angle \mathit{BAD}$为“黄金角”， $\mathit{AB}<\mathit{AD}$，若 $\mathit{AD}=1$，则 $\mathit{AC}=$　　．

【问题探究】（2）如图2，在四边形 $\mathit{ABCD}$中， $\mathit{BC}//\mathit{AD}$， $\angle \mathit{BAC}=\angle \mathit{DAC}=\angle D=36°$．求证：四边形 $\mathit{ABCD}$为“黄金四边形”．

【拓展延伸】（3）如图3，在“黄金四边形” $\mathit{ABC}{A}_1$中， $\angle \mathit{BA}{A}_1$为“黄金角”， $\mathit{AB}<A{A}_1$，在四边形 $\mathit{ABC}{A}_1$外部依次作△ $A{A}_1{A}_2$，△ $A{A}_2{A}_3$， $\dots$，使四边形 $\mathit{AC}{A}_1{A}_2$， $A{A}_1{A}_2{A}_3$， $\dots$均为“黄金四边形”，且满足 $\angle \mathit{CA}{A}_2$， $\angle A_{n}A{A}_{n+2}(n=1$，2， $3\dots )$均为“黄金角”， $A{A}_n<A{A}_{n+1}(n=1$，2， $3\dots )$

①若 $\mathit{AC}=1$，则第 $n$个“黄金四边形”中， $A{A}_n=$　　（用含 $n$的式子表示）．

②若“黄金角” $\angle \mathit{BA}{A}_1=80°$，则当 $A$， $B$， $A_n$三点第一次在同一条直线上时， $n=$　　．

如图，在 $\mathit{\Delta ABC}$中，点 $D$， $E$分别在边 $\mathit{AB}$， $\mathit{AC}$上， $\angle \mathit{AED}=\angle B$，射线 $\mathit{AG}$分别交线段 $\mathit{DE}$， $\mathit{BC}$于点 $F$， $G$，且 $\frac{\mathit{AD}}{\mathit{AC}}=\frac{\mathit{DF}}{\mathit{CG}}$．

（1）求证： $\mathit{\Delta ADF}\backsim \mathit{\Delta ACG}$；

（2）若 $\frac{\mathit{AD}}{\mathit{AC}}=\frac{1}{2}$，求 $\frac{\mathit{AF}}{\mathit{FG}}$的值．

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$．

（1）作出经过点 $B$，圆心 $O$在斜边 $\mathit{AB}$上且与边 $\mathit{AC}$相切于点 $E$的 $\odot O$（要求：用尺规作图，保留作图痕迹，不写作法和证明）

（2）设（1）中所作的 $\odot O$与边 $\mathit{AB}$交于异于点 $B$的另外一点 $D$，若 $\odot O$的直径为5， $\mathit{BC}=4$；求 $\mathit{DE}$的长．（如果用尺规作图画不出图形，可画出草图完成（2）问）

已知：如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ACB}=90°$，点 $M$是斜边 $\mathit{AB}$的中点， $\mathit{MD}//\mathit{BC}$，且 $\mathit{MD}=\mathit{CM}$， $\mathit{DE}\perp \mathit{AB}$于点 $E$，连接 $\mathit{AD}$、 $\mathit{CD}$．

（1）求证： $\mathit{\Delta MED}\backsim \mathit{\Delta BCA}$；

（2）求证： $\mathit{\Delta AMD}\cong \mathit{\Delta CMD}$；

（3）设 $\mathit{\Delta MDE}$的面积为 $S_1$，四边形 $\mathit{BCMD}$的面积为 $S_2$，当 $S_2=\frac{17}{5}{S}_1$时，求 $\cos \angle \mathit{ABC}$的值．

如图， $\mathit{AB}$为圆 $O$的直径， $C$为圆 $O$上一点， $D$为 $\mathit{BC}$延长线一点，且 $\mathit{BC}=\mathit{CD}$， $\mathit{CE}\perp \mathit{AD}$于点 $E$．

（1）求证：直线 $\mathit{EC}$为圆 $O$的切线；

（2）设 $\mathit{BE}$与圆 $O$交于点 $F$， $\mathit{AF}$的延长线与 $\mathit{CE}$交于点 $P$，已知 $\angle \mathit{PCF}=\angle \mathit{CBF}$， $\mathit{PC}=5$， $\mathit{PF}=4$，求 $\sin \angle \mathit{PEF}$的值．

如图，过 $\odot O$外一点 $P$作 $\odot O$的切线 $\mathit{PA}$切 $\odot O$于点 $A$，连接 $\mathit{PO}$并延长，与 $\odot O$交于 $C$、 $D$两点， $M$是半圆 $\mathit{CD}$的中点，连接 $\mathit{AM}$交 $\mathit{CD}$于点 $N$，连接 $\mathit{AC}$、 $\mathit{CM}$．

（1）求证： $C{M}^2=\mathit{MN}\cdot \mathit{MA}$；

（2）若 $\angle P=30°$， $\mathit{PC}=2$，求 $\mathit{CM}$的长．