已知 中, ,点 、 分别在 、 边上,连接 、 交于点 ,设 , , 为常数,试探究 的度数:
(1)如图1,若 ,则 的度数为 ;
(2)如图2,若 ,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出 的度数.
(3)如图3,若 ,且 、 分别在 、 的延长线上,(2)中的结论是否成立,请说明理由.

阅读下面材料:
小明遇到这样一个问题:如图1, 中, ,点 在 边上, , ,垂足为 ,求证: .
小明经探究发现,过点 作 ,垂足为 ,得到 ,从而可证 (如图 ,使问题得到解决.
(1)根据阅读材料回答: 与 全等的条件是 (填“ ”、“ ”、“ ”、“ ”或“ ”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3, 中, , , 为 的中点, 为 的中点,点 在 的延长线上,且 ,若 ,求 的长;
(3)如图4, 中, , ,点 、 分别在 、 边上,且 (其中 , ,求 的值(用含 的式子表示).

如图, 是 直径,弦 ,垂足为点 .弦 交 于点 ,点 在 延长线上,且 .
(1)求证: 为 切线;
(2)若 , , ,求 的长.

已知, 为直角三角形, ,点 是射线 上一点(点 不与点 、 重合),线段 绕点 顺时针旋转 得到线段 ,连接 交射线 于点 .
(1)如图①,当 ,点 在线段 上时,线段 、 的数量关系是 ;
(2)如图②,当 ,点 在线段 的延长线时,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由.
(3)如图③,若
,点
在线段
的延长线上,
,
,求
的面积.
如图1, 是 的直径 上的一点,过 作 交 于 、 , 是 上的一点,过 的直线分别与 、 的延长线相交于 、 ,连接 交 于 , .
(1)求证: 是 的切线;
(2)若 , 的半径为4, ,求 的长;
(3)如图2,在(2)的条件下,连接 、 ;在线段 上有一点 ,并且以 、 、 为顶点的三角形与 相似,求 的长度.

如图, 中, 为钝角, ,点 是边 延长线上一点,以点 为顶点, 为边,在射线 下方作 .
(1)在射线 上取点 ,连接 交线段 于点 .
①如图1,若 ,请直接写出线段 与 的数量关系和位置关系;
②如图2,若 ,判断线段 与 的数量关系和位置关系,并说明理由;
(2)如图3,反向延长射线 ,交射线 于点 ,将 沿 方向平移,使顶点 落在点 处,记平移后的 为 ,将 绕点 顺时针旋转角 , 交线段 于点 , 交射线 于点 ,请直接写出线段 , 与 之间的数量关系.

如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.
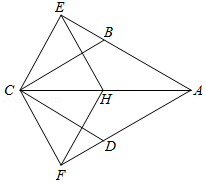
如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
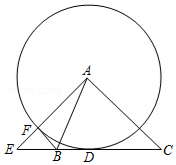
如图,在四边形 中, ,过点 作 于 ,若 .
(1)求证: ;
(2)连接 交 于点 ,若 , ,求 的长.

阅读与思考
请阅读下列科普材料,并完成相应的任务.
图算法 图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系: 得出,当 时, .但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种根据特制的线条进行计算的方法就是图算法. 再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少? 我们可以根据公式 求得 的值,也可以设计一种图算法直接得出结果:我们先来画出一个 的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值. 图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性. |
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性:
①用公式 计算:当 , 时, 的值为多少;
②如图,在 中, , 是 的角平分线, , ,用你所学的几何知识求线段 的长.

如图, 为线段 上一点,以 为圆心, 长为半径的 交 于点 ,点 在 上,连接 ,满足 .
(1)求证: 是 的切线;
(2)若 ,求 的值.
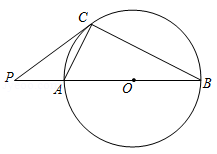
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.
