初中数学相似三角形的判定与性质解答题

（年贵州省铜仁市）如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．

（1）求证：CB平分∠ACE；
（2）若BE=3，CE=4，求⊙O的半径．

（年江西省南昌市）我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．
特例探索
（1）如图1，当∠ABE=45°，c=时，a=       ，b=       ．
如图2，当∠ABE=30°，c=4时，a=       ，b=       ．
归纳证明
（2）请你观察（1）中的计算结果，猜想，，三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．
拓展应用
（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=，AB=3，求AF的长．

（年青海省中考）如图，二次函数的图象与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．该抛物线的顶点为M．

（1）求该抛物线的解析式；
（2）判断△BCM的形状，并说明理由；
（3）探究坐标轴上是否存在点P，使得以点P、A、C为顶点的三角形与△BCM相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．

（年贵州省黔南州）如图，在平面直角坐标系xOy中，抛物线过点A（0，4）和C（8，0），P（t，0）是x轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB，过点B作x轴的垂线，过点A作y轴的垂线，两直线交于点D．

（1）求b、c的值；
（2）当t为何值时，点D落在抛物线上；
（3）是否存在t，使得以A，B，D为顶点的三角形与△AOP相似？若存在，求此时t的值；若不存在，请说明理由．

（年云南省）如图，在平面直角坐标系中，抛物线（）与x轴相交于A，B两点，与y轴相交于点C，直线（）经过B，C两点，已知A（1，0），C（0，3），且BC=5．

（1）分别求直线BC和抛物线的解析式（关系式）；
（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

（年 呼 和 浩 特 市）如图，⊙O是△ABC的外接圆，P是⊙O外的一点，AM是⊙O的直径，∠PAC=∠ABC
（1）求证：PA是⊙O的切线；
（2）连接PB与AC交于点D，与⊙O交于点E，F为BD上的一点，若M为的中点，且∠DCF=∠P，求证：

（内蒙古 呼 和 浩 特 ）如图，⊙O是△ABC的外接圆，P是⊙O外的一点，AM是⊙O的直径，∠PAC=∠ABC
（1）求证：PA是⊙O的切线；
（2）连接PB与AC交于点D，与⊙O交于点E，F为BD上的一点，若M为的中点，且∠DCF=∠P，求证：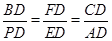

（贵州六盘水）（本小题12分）如图，在Rt△ACB中，∠ACB＝90°，点O是AC边上的一点，以O为圆心，OC为半径的圆与AB相切于点D，连接OD．
（1）△ADO∽△ACB．
（2）若⊙O的半径为1，求证：AC＝AD·BC

（年青海西宁12分）如图，抛物线交x轴于A，B两点（点A在点B的左侧），交y轴于点C，分别过点B，C作y轴，x轴的平行线，两平行线交于点D，将△BDC绕点C逆时针旋转，使点D旋转到y轴上得到△FEC，连接BF．

（1）求点B，C所在直线的函数解析式；
（2）求△BCF的面积；
（3）在线段BC上是否存在点P，使得以点P，A，B为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．