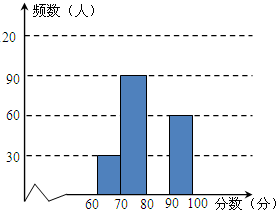
2015年是中国抗日战争胜利70周年暨世界反法西斯战争胜利70周年.某校为纪念中国抗日战争胜利70周年,对全校学生进行了“抗日战争知多少”知识测验.然后随机抽取了部分学生的成绩,整理并制作如图所示的图表.
请你根据图表中提供的信息,解答下列问题:
分数段
|
频数
|
频率
|
60≤x<70
|
30
|
0.1
|
70≤x<80
|
90
|
m
|
80≤x<90
|
n
|
0.4
|
90≤x<100
|
60
|
0.2
|
(1)在频数分布表中: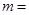 ________,
________,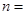 ________;
________;
(2)补全频数分布直方图;
(3)如果某校有2000名学生,比赛成绩80分以上(含80分)为优秀,那么你估计此次测验成绩的优秀人数大约是__________人.