如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.
推荐套卷
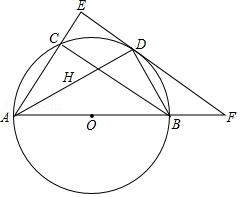
如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.
