如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图,在 中, , 与 , 分别相切于点 , , 平分 ,连接 .
(1)求证: 是 的切线;
(2)若 , 的半径是1,求图中阴影部分的面积.

如图, 是等边 的内切圆,分别切 , , 于点 , , , 是 上一点,则 的度数是
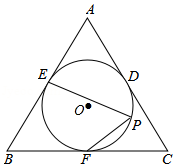
A. B. C. D.
如图,矩形 中, 是 的中点,过 、 、 三点的圆 与边 、 分别交于点 、点 ,给出下列说法:(1) 与 的交点是圆 的圆心;(2) 与 的交点是圆 的圆心;(3) 与圆 相切,其中正确说法的个数是

A.0B.1C.2D.3
结果如此巧合
下面是小颖对一道题目的解答.
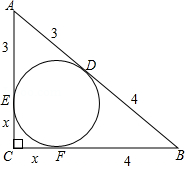
题目:如图, 的内切圆与斜边 相切于点 , , ,求 的面积.
解:设 的内切圆分别与 、 相切于点 、 , 的长为 .
根据切线长定理,得 , , .
根据勾股定理,得 .
整理,得 .
所以
.
小颖发现12恰好就是 ,即 的面积等于 与 的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知: 的内切圆与 相切于点 , , .
可以一般化吗?
(1)若 ,求证: 的面积等于 .
倒过来思考呢?
(2)若 ,求证 .
改变一下条件
(3)若 ,用 、 表示 的面积.
如图,已知 , .
(1)在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);
(2)连接 , ,求 的度数.

如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.

如图,四边形 内接于 ,点 是 的内心, ,点 在 的延长线上,则 的度数为
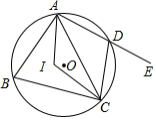
A. B. C. D.
如图,在平面直角坐标系 中, , , , 是 的内心,将 绕原点逆时针旋转 后, 的对应点 的坐标为
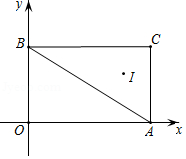
A. B. C. D.