如图, 是 的外接圆, 为 的直径,点 为 的内心,连接 并延长交 于 点,连接 并延长至 ,使得 ,连接 、 .
(1)求证: ;
(2)求证:直线 为 的切线.
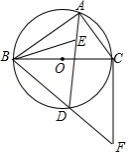
如图,在矩形 中,对角线相交于点 , 为 的内切圆,切点分别为 , , , , .
(1)求 , ;
(2)点 从点 出发,沿线段 向点 以每秒3个单位长度的速度运动,当点 运动到点 时停止,过点 作 交 于点 ,设运动时间为 秒.
①将 沿 翻折得△ ,是否存在时刻 ,使点 恰好落在边 上?若存在,求 的值;若不存在,请说明理由;
②若点 为线段 上的动点,当 为正三角形时,求 的值.
如图,点 是 的内心, 的延长线交 于点 ,交 的外接圆 于点 ,连接 ,过点 作直线 ,使 .
(1)求证:直线 是 的切线;
(2)求证: .

《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”

A.3步B.5步C.6步D.8步
我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
(2)如图, 中, ,点 在 上,且 ,求证: 是 的“内似线”;
(3)在 中, , , , 、 分别在边 、 上,且 是 的“内似线”,求 的长.

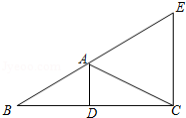
如图,在 中, 是边 上的中线, , , 交 的延长线于点 , , .
(1)求 的长;
(2)求证: 为等腰三角形.
(3)求 的外接圆圆心 与内切圆圆心 之间的距离.
如图,在 中, , , .按以下步骤作图:
①以 为圆心,任意长为半径作弧,分别交 , 于点 , ;
②分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;
③作射线 ;
④以同样的方法作射线 .
交 于点 ,连接 ,则 .

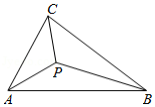
如图, 是 的内心,连接 、 、 , 、 、 的面积分别为 、 、 .则 .(填“ ”或“ ”或“ ”
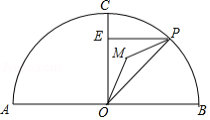
如图, 为 的直径,且 ,点 在半圆上, ,垂足为点 , 为半圆上任意一点(不与点 重合),过 点作 于点 ,设 的内心为 ,连接 、 .
(1)求 的度数;
(2)当点 在半圆上从点 运动到点 时,求内心 所经过的路径长.
如图,矩形 中, , ,连接 , 和 分别是 和 的内切圆,则 的长是

A. B. C. D.