已知 的内切圆 与 、 、 分别相切于点 、 、 ,若 ,如图1.
(1)判断 的形状,并证明你的结论;
(2)设 与 相交于点 ,如图2, ,求 的长.

阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为 , , ,记 ,那么三角形的面积为 . ①
古希腊几何学家海伦 ,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约 约 ,曾提出利用三角形的三边求面积的秦九韶公式: . ②
下面我们对公式②进行变形: .
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦 秦九韶公式.
问题:如图,在 中, , , , 内切于 ,切点分别是 、 、 .
(1)求 的面积;
(2)求 的半径.

如图,在 中, , ,点 是 边上的一点, ,设 与 的内切圆半径分别为 , ,那么

A.2B. C. D.
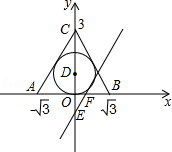
在平面直角坐标系中,△ABC三个顶点坐标为 、 、
(1)求△ABC内切圆⊙D的半径.
(2)过点 的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
(3)以(2)为条件,P为直线EF上一点,以P为圆心,以 为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
(1)求证: ;
(2)求证: .

《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是 步.
如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )

A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
如图1,在△ ABC中, AB= AC,⊙ O是△ ABC的外接圆,过点 C作∠ BCD=∠ ACB交⊙ O于点 D,连接 AD交 BC于点 E,延长 DC至点 F,使 CF= AC,连接 AF.
(1)求证: ED= EC;
(2)求证: AF是⊙ O的切线;
(3)如图2,若点 G是△ ACD的内心, BC• BE=25,求 BG的长.

如图,以Rt△ ABC的直角边 AB为直径的⊙ O交斜边 AC于点 D,过点 D作⊙ O的切线与 BC交于点 E,弦 DM与 AB垂直,垂足为 H.
(1)求证: E为 BC的中点;
(2)若⊙ O的面积为12π,两个三角形△ AHD和△ BMH的外接圆面积之比为3,求△ DEC的内切圆面积 S 1和四边形 OBED的外接圆面积 S 2的比.

如图,在圆心角为90°的扇形 OAB中, OB=2, P为 上任意一点,过点 P作 PE⊥ OB于点 E,设 M为△ OPE的内心,当点 P从点 A运动到点 B时,则内心 M所经过的路径长为 .

如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若 ,则∠BEC的度数为 .

如图,△ ABC是一块绿化带,将阴影部分修建为花圃,已知 AB=15, AC=9, BC=12,阴影部分是△ ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图 ,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为
,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为 ,
,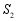 ,
,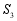 ,
, ,
,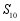 ,则
,则 .
.

已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式 (其中a,b,c是三角形的三边长, ,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴
∴
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
根据上述材料,解答下列问题:
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
