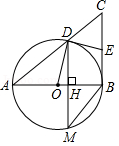
如图,以Rt△ ABC的直角边 AB为直径的⊙ O交斜边 AC于点 D,过点 D作⊙ O的切线与 BC交于点 E,弦 DM与 AB垂直,垂足为 H.
(1)求证: E为 BC的中点;
(2)若⊙ O的面积为12π,两个三角形△ AHD和△ BMH的外接圆面积之比为3,求△ DEC的内切圆面积 S 1和四边形 OBED的外接圆面积 S 2的比.
相关知识点
推荐套卷
如图,以Rt△ ABC的直角边 AB为直径的⊙ O交斜边 AC于点 D,过点 D作⊙ O的切线与 BC交于点 E,弦 DM与 AB垂直,垂足为 H.
(1)求证: E为 BC的中点;
(2)若⊙ O的面积为12π,两个三角形△ AHD和△ BMH的外接圆面积之比为3,求△ DEC的内切圆面积 S 1和四边形 OBED的外接圆面积 S 2的比.
