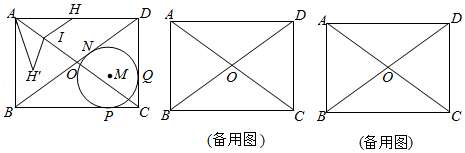
如图,在矩形 中,对角线相交于点 , 为 的内切圆,切点分别为 , , , , .
(1)求 , ;
(2)点 从点 出发,沿线段 向点 以每秒3个单位长度的速度运动,当点 运动到点 时停止,过点 作 交 于点 ,设运动时间为 秒.
①将 沿 翻折得△ ,是否存在时刻 ,使点 恰好落在边 上?若存在,求 的值;若不存在,请说明理由;
②若点 为线段 上的动点,当 为正三角形时,求 的值.
问题提出
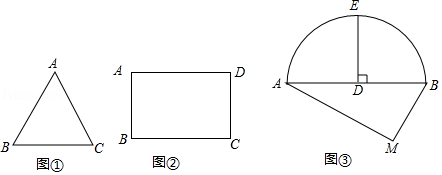
(1)如图①,是等边三角形,
,若点
是
的内心,则
的长为 ;
问题探究
(2)如图②,在矩形中,
,
,如果点
是
边上一点,且
,那么
边上是否存在一点
,使得线段
将矩形
的面积平分?若存在,求出
的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由草地和弦
与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在
处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于
(即每次喷灌时喷灌龙头由
转到
,然后再转回,这样往复喷灌.
同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出,
,
的面积为
;过弦
的中点
作
交
于点
,又测得
.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
如图,顶点为的抛物线
与
轴交于
,
两点,与
轴交于点
.
(1)求这条抛物线对应的函数表达式;
(2)问在轴上是否存在一点
,使得
为直角三角形?若存在,求出点
的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点,满足
,过
作
轴于点
,设
的内心为
,试求
的最小值.
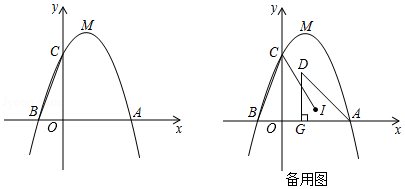
结果如此巧合
下面是小颖对一道题目的解答.
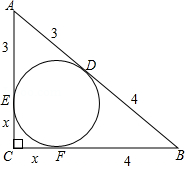
题目:如图, 的内切圆与斜边 相切于点 , , ,求 的面积.
解:设 的内切圆分别与 、 相切于点 、 , 的长为 .
根据切线长定理,得 , , .
根据勾股定理,得 .
整理,得 .
所以
.
小颖发现12恰好就是 ,即 的面积等于 与 的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知: 的内切圆与 相切于点 , , .
可以一般化吗?
(1)若 ,求证: 的面积等于 .
倒过来思考呢?
(2)若 ,求证 .
改变一下条件
(3)若 ,用 、 表示 的面积.
如图, 是等边 的内切圆,分别切 , , 于点 , , , 是 上一点,则 的度数是
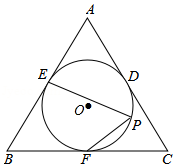
A. B. C. D.
如图,已知 , .
(1)在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);
(2)连接 , ,求 的度数.

如图,在直角三角形 中, ,点 是 的内心,
的延长线和三角形 的外接圆 相交于点 ,连接 .
(1)求证: ;
(2)过点 作 的平行线交 、 的延长线分别于点 、 ,已知 ,圆 的直径为5.
①求证: 为圆 的切线;
②求 的长.

如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图,四边形 内接于 ,点 是 的内心, ,点 在 的延长线上,则 的度数为
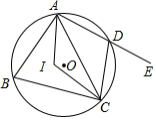
A. B. C. D.
如图,矩形 中, 是 的中点,过 、 、 三点的圆 与边 、 分别交于点 、点 ,给出下列说法:(1) 与 的交点是圆 的圆心;(2) 与 的交点是圆 的圆心;(3) 与圆 相切,其中正确说法的个数是

A.0B.1C.2D.3