如图,将矩形纸片 沿直线 折叠,顶点 恰好与 边上的动点 重合(点 不与点 , 重合),折痕为 ,点 , 分别在边 , 上,连接 , , , 与 相交于点 .
(1)求证: ;
(2)①在图2中,作出经过 , , 三点的 (要求保留作图痕迹,不写做法);
②设 ,随着点 在 上的运动,若①中的 恰好与 , 同时相切,求此时 的长.

如图,在 中, , 是 的平分线,以 为直径的 交 边于点 ,连接 ,过点 作 ,交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
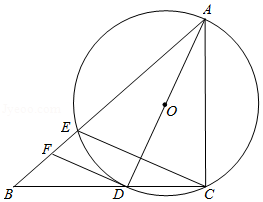
如图, 是 的外接圆, 点在 边上, 的平分线交 于点 ,连接 、 ,过点 作 的平行线,与 的延长线相交于点 .
(1)求证: 是 的切线;
(2)求证: ;
(3)当 , 时,求线段 的长.

如图,过 外一点 作 的切线 切 于点 ,连接 并延长,与 交于 、 两点, 是半圆 的中点,连接 交 于点 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的长.

某学习小组的学生在学习中遇到了下面的问题:
如图1,在
和
中,
,
,点
,
,
在同一条直线上,连接
,点
是
的中点,连接
,
,试判断
的形状并说明理由.
问题探究:
(1)小婷同学提出解题思路:先探究 的两条边是否相等,如 ,以下是她的证明过程
证明:延长线段 交 的延长线于点 . 是 的中点, . , . |
. 又 , . . . |
请根据以上证明过程,解答下列两个问题:
①在图1中作出证明中所描述的辅助线;
②在证明的括号中填写理由(请在 , , , 中选择).
(2)在(1)的探究结论的基础上,请你帮助小婷求出 的度数,并判断 的形状.
问题拓展:
(3)如图2,当 绕点 逆时针旋转某个角度时,连接 ,延长 交 的延长线于点 ,其他条件不变,判断 的形状并给出证明.
如图,在正方形 中,点 在 边上,连接 , 的平分线 与 边交于点 ,与 的延长线交于点 .设 .
(1)若 , ,求线段 的长.
(2)连接 ,若 ,
①求证:点 为 边的中点.
②求 的值.

正方形 的边长为 ,点 、 分别是线段 、 上的动点,连接 并延长,交边 于 ,过 作 ,垂足为 ,交边 于点 .

(1)如图1,若点 与点 重合,求证: ;
(2)如图2,若点 从点 出发,以 的速度沿 向点 运动,同时点 从点 出发,以 的速度沿 向点 运动,运动时间为 .
①设 ,求 关于 的函数表达式;
②当 时,连接 ,求 的长.
如图, 是 上一点,点 在直径 的延长线上, 的半径为3, , .
(1)求证: 是 的切线.
(2)求 的值.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
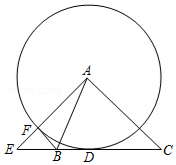
如图,在四边形 中, ,过点 作 于 ,若 .
(1)求证: ;
(2)连接 交 于点 ,若 , ,求 的长.

阅读与思考
请阅读下列科普材料,并完成相应的任务.
图算法 图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系: 得出,当 时, .但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种根据特制的线条进行计算的方法就是图算法. 再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少? 我们可以根据公式 求得 的值,也可以设计一种图算法直接得出结果:我们先来画出一个 的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值. 图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性. |
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性:
①用公式 计算:当 , 时, 的值为多少;
②如图,在 中, , 是 的角平分线, , ,用你所学的几何知识求线段 的长.

如图, 为线段 上一点,以 为圆心, 长为半径的 交 于点 ,点 在 上,连接 ,满足 .
(1)求证: 是 的切线;
(2)若 ,求 的值.
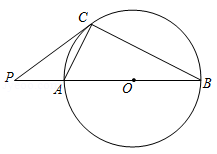
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.
