初中数学圆解答题

梯形ABCD中DC∥AB， AB =2DC，对角线AC、BD相交于点O， BD=4，过AC的中点H作EF∥BD分别交AB、AD于点E、F，求EF的长.

 

（本题8分）如图，四边形中，，平分，交于.

（1）求证：四边形是菱形；
（2）若点是的中点，试判断的形状，并说明理由.

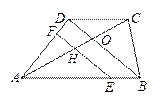．已知：如图，梯形ABCD中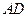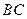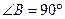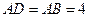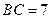，∥，，，，点E在BC边上，将△CDE沿DE折叠，点C恰好落在AB边上的点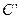处．

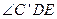（1）求的度数；
（2）求△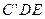的面积．

如图，在梯形ABCD中，AD∥BC，∠B=60°，∠ADC=105°，AD=6，且AC⊥AB，求AB的长．

如图，在梯形ABCD中，AD∥BC，∠B=60°，∠ADC=105°，AD=6，且AC⊥AB，求AB的长．

(10分)已知：如图，ABCD是平行四边形，P是CD上的一点，且AP和BP分别平分∠DAB和∠CBA，过点P作AD的平行线，交AB于点Q.(1)求证：AP⊥PB；
　　(2)若AD=5cm，AP=8cm，求AB的长及△APB的面积.
　　

(10分)已知：在△ABC中，AC=BC，D，E，F分别是AB，AC，CB的中点.
　　求证：四边形DECF是菱形.
　　

(1)如图1，在正方形ABCD中，点E、F分别在边BC，CD上，AE，BF交于点O，∠AOF=90°.求证：BE=CF.
　　(2)如图2，在正方形ABCD中，点E，H，F，G分别在边AB，BC，CD，DA上，EF，GH交于点O，∠FOH=90°，EF=4.求GH的长.
　　　　
　　(3)已知点E，H，F，G分别在矩形ABCD的边AB，BC，CD，DA上，EF，GH交于点O，∠FOH=90°，EF=4.直接写出下列两题的答案：
　　①如图3，矩形ABCD由2个全等的正方形组成，GH=____.
　　②如图4，矩形ABCD由n个全等的正方形组成，GH=____(用含n的代数式表示)
　　

如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE.我们探究下列图中线段BG、DE的长度关系及所在直线的位置关系：

　　(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系(直接写出答案)；
　　②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α得到图2，图3的情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断.
　　(2)在第(1)题图2中，连接DG、BE，且AB=3，EF=2，求BE2+DG2的值.

如图23，ABCD为正方形，E为BC上一点，将正方形折叠，使A点与E点重合，折痕为MN，若。

（1）求△ANE的面积；
（2）求sin∠ENB的值。

如图，在梯形中，，，，在上截取，使，过点作于，交于点，连接，交于点，交于点。

（1）求证：
（2）已知，，求的长。

如图，梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD相交于O，且AC⊥BD，若AD＋BC=4cm，求：

（1）对角线AC的长；
（2）梯形ABCD的面积．

如图，矩形ABCD的对角线相交于点O，DE//AC，CE//DB，CE、DE交于点E，请问：四边形DOCE是什么四边形?请说明理由。

已知如图，平行四边形ABCD的对角线AC、BD相交于点O，M、N分别 是OA、OC的中点. 求证：BM="DN" .

如图，菱形ABCD的边长为20cm，∠ABC＝120°．动点P、Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q以2cm/s的速度，沿A→C的路线向点C运动．当P、Q到达终点C时，整个运动随之结束，设运动时间为t秒．

（1）在点P、Q运动过程中，请判断PQ与对角线AC的位置关系，并说明理由；
（2）若点Q关于菱形ABCD的对角线交点O的对称点为M，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N．
①当t为何值时，点P、M、N在一直线上？
②当点P、M、N不在一直线上时，是否存在这样的t，使得△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．