初中数学圆解答题

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E， 连接DE，F为线段DE上一点，且∠AFE=∠B．

(1)求证：△ADF∽△DEC
(2)若AB=4，AD=3，AE=3，求AF的长．

如图5，在梯形ABCD中，AB∥DC， DB平分∠ADC，过点A作AE∥BD，交CD的
延长线于点E，且∠C＝2∠E．

（1）求证：梯形ABCD是等腰梯形．
（2）若∠BDC＝30°，AD＝5，求CD的长．

如图，四边形ABCD是菱形，点E、F分别是边AD、CD的中点.求证：BE=BF.

如图，在ABCD的各边AB、BC、CD、DA上，分别取点K、L、M、N，使AK=CM、BL=DN，求证：四边形KLMN为平行四边形。

已知：在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD,AD=3cm,BC=7cm,求梯形的高

如图7，在梯形ABCD中，AD∥BC, ，．
（1）求证：
（2）若，求梯形ABCD的面积

如图①，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O。

（1）判断四边形ABCE是怎样的四边形，说明理由；
（2）如图②，P是线段BC上一动点（不与点B、C重合），连接PO并延长交线段AB于点Q，QR⊥BD，垂足为点R。四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积。

如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AB，BD， BC，AC的中点。

（1）求证：四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并证明你的结论。

如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是线段BC上一点，以AE为边在直线MN的上方作正方形AEFG

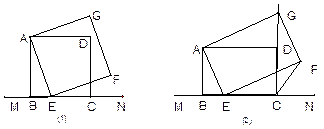
连结GD，求证△ADG≌△ABE；
如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=1,BC=2，E是线段BC上一动点（不含端点B,C ）,以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当E由B向C运动时，∠FCN的大小是否保持不变，若∠FCN的大小不变，求tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．

如图，梯形ABCD中，AB//CD，E是BC的中点，直线AE交DC的延长线于F
求证：≌

如图11，正方形ABCD的边长为5，点F为正方形ABCD内的点，△BFC经逆时针旋转后能与△BEA重合.

（1）旋转中心是哪一点？旋转了多少度？
（2）判断△BEF是怎样的三角形？并说明理由；
（3）若BE=3，FC=4，说明AE∥BF.

如图10，在梯形ABCD中，AD∥BC，AB= DC=1，BD平分∠ABC，BD⊥CD.

（1）求：① ∠BAD的度数；② BD的长；
（2）延长BC至点E，使CE=CD，说明△DBE是等腰三角形

如图，有两个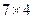的网格，网格中每个小正方形的边长均为1，每个网格中各画有一个梯形．请在图1、图2中分别画出一条线段，同时满足以下要求：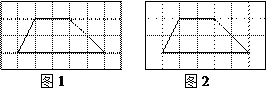

（1）线段的一个端点为梯形的顶点，另一个端点在梯形一边的格点上；
（2）将梯形分成两个图形，其中一个是轴对称图形；
（3）图1、图2中分成的轴对称图形不全等．

如图，在梯形ABCD中，AB‖CD，∠A=，AB=3，CD=6，BE⊥BC交直线AD于点E.

（1）当点E与D恰好重合时，求AD的长；
（2）当点E在边AD上时（E不与A、D重合），设AD=x，ED=y，试求y关于x的函数关系式，并写出定义域；
（3）问：是否可能使△ABE、△CDE与△BCE都相似？若能，请求出此时AD的长；若不能，请说明理由.

如图，将正方形纸片的两角分别折叠，使顶点A落在A′处，顶点D落在D′处，BC、BE为折痕，点B、A′、D′在同一条直线上。

（1）猜想折痕BC和BE的位置关系，并说明理由；
（2）写出图中∠D′BE的余角与补角；
（3）延长D′B、CA相交于点F，若∠EBD=330，求∠ABF和∠CBA的度数。