辽宁省凌海市初三上学期期末数学卷
用四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
| A.0.1(精确到0.1) | B.0.05(精确到百分位) |
| C.0.05(精确到千分位) | D.0.0502(精确到0.0001) |
下列说法中,正确的有( )
① 成立
成立
②若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补
③连结两点的线段叫做两点的距离
④若点B是线段AC的中点,则AB=BC
| A.1个 | B.2个 | C.3个 | D.4个 |
元旦期间,七(1)班的明明、丽丽等同学随家长一同到某公园游玩,下面是购买门票时,明明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴ 明明他们一共去了几个成人,几个学生?
⑵ 请你帮助明明算一算,用哪种方式购票更省钱?说明理由。
⑶ 购完票后,明明发现七(2)班的张小涛等8名同学和他们的12名家长共20人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.
如图,△ABC中,∠ACB=90°, ∠A=30°AC的中垂线交AC于E.交AB于D,则图中60°的角共有 ( )
| A.6个 | B.5个 | C.4个 | D.3个 |
方程x2-2(3x-2)+(x+1)=0的一般形式是 ( )
| A.x2-5x+5=0 | B.x2+5x+5="0" | C.x2+5x-5=0 | D.x2+5=0 |
如图是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标,猜测比较合理的是 ( )
| A.小明:“早上8点” | B.小亮:“中午12点” |
| C.小刚:“下午5点” | D.小红:“什么时间都行” |
甲乙两地相距100km,汽车从甲地开往乙地,所需时间t(小时)和速度v(km/h)之间的函数关系图象大致是下图中( )
若梯形中位线的长是高的2倍,梯形的面积是18cm2,则这个梯形的高等于
| A.6cm | B.6 cm | C.3cm | D.3 cm |
在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于 
| A.1 | B. |
C. |
D. |
如图,在△ABC中,AB=AC=BD,AD=CD,则∠ADB的度数是( )
| A.36° | B.45° | C.60° | D.72° |
△ABC中,∠A,∠B均为锐角,且有 ,则△ABC是( )
,则△ABC是( )
| A.直角(不等腰)三角形 | B.等腰直角三角形 |
| C.等腰(不等边)三角形 | D.等边三角形 |
某商品成本价为300元,两次降价后现价为160元,若每次降价的百分率相同,设降价的百分率为x,则方程为__________
为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有______个白球
已知:如图梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O,写出图中的全等三角形:___________
如图△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=1,那么PP′有长等于__________
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD, BC,AC的中点。
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论。
为了加快城市经济发展,某市准备修建一座横跨南北的大桥.如图10所示,测量队在点A处观测河对岸水边有一点C,测得C在北偏东60°的方向上,沿河岸向东前行30米到达B处,测得C在北偏东45°的方向上,请你根据以上数据帮助该测量队计算出这条河的宽度(结果保留根号)。
某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑。希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑。
(1) 写出所有选购方案(利用树状图或列表方法表示);
(2) 如果(1)中各种选购方案被选中的可能性相同,那么B型号电脑被选中的概率是多少?
如图所示,在Rt△ABC中,∠B=90°,AB=18cm,BC=36cm,一点P从A沿AB边以2cm/s的速度向B点移动;点Q从B点开始沿BC边以6cm/s的速度向C点移动。如果P、Q两点同时出发,求几秒后Rt△BPQ的面子等于Rt△ABC的面积的

将一条长20cm的铁丝剪成两段,然后每一条铁丝的长度为周长做成正方形,
(1)要使这两个正方形的面积之和为17cm2 , 那么这段铁丝被剪成的两段长度分别是多少?
(2)两个正方形的面积之和可能为12cm2 吗?若能,请求出两段铁丝的长度;若不能,请说明理由。
已知:如图所示,D、E、F分别是△ABC的三边上的点,且CE=BF,△DCE和△DBF的面积相等。求证:AD平分∠BAC
如图,已知反比例函数y= 的图象经过点A(-
的图象经过点A(- ,b),过点A作AB⊥x轴于B,△AOB的面积为
,b),过点A作AB⊥x轴于B,△AOB的面积为 。
。
(1) ;
;
(2)若一次函数y=ax+1的图象经过点A,且与 轴交于M,求AO∶AM;
轴交于M,求AO∶AM;
(3)若反比例函数的图象与一次函数的图象的另一个交点为C,求C的坐标
 的解为( )
的解为( )  是( )
是( ) 时,去分母正确的是( )
时,去分母正确的是( )
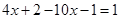
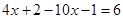


 的值为3,则
的值为3,则 的值为( )
的值为( )

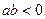
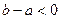

 =20°32′,则∠
=20°32′,则∠ 与
与 是同类项,则m-n=
是同类项,则m-n= 
 ,…中,发现规律得到巴尔末公式,从而打开了光谱奥妙的大门,请按这种规律写出第7个数据是______
,…中,发现规律得到巴尔末公式,从而打开了光谱奥妙的大门,请按这种规律写出第7个数据是______

 其中
其中 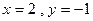
 的值为0,则x的值为
的值为0,则x的值为 



 粤公网安备 44130202000953号
粤公网安备 44130202000953号