2008年高级中等学校招生全国统一考试数学卷(广东深圳)
如图,直线 分别与x轴、y轴交于A、B两点;直线
分别与x轴、y轴交于A、B两点;直线 与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位
与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位 ),点E的运动时间为t(秒).
),点E的运动时间为t(秒).
⑴求点C的坐标.
⑵当0<t<5时,求S与t之间的函数关系式.
⑶求⑵中S的最大值.
⑷当t>0时,直接写出点(4, )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
反比例函数 的图象经过点
的图象经过点 ,则该反比例函数图象在( )
,则该反比例函数图象在( )
| A.第一、三象限 | B.第二、四象限 |
| C.第二、三象限 | D.第一、二象限 |
国家体育场“鸟巢”建筑面积达25.8万平方米,将25.8万平方米用科学记数法(四舍五入保留2个有效数字)表示约为( )
| A.26×104平方米 | B.2.6×104平方米 |
| C.2.6×105平方米 | D.2.6×106平方米 |
下列说法正确的是( )
| A.某市“明天降雨的概率是75%”表示明天有75%的时间会降雨 |
| B.随机抛掷一枚均匀的硬币,落地后正面一定朝上 |
C.在一次抽奖活动中,“中奖的概率是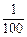 ”表示抽奖l00次就一定会中奖 ”表示抽奖l00次就一定会中奖 |
| D.在平面内,平行四边形的两条对角线一定相交 |
如图(图在第二页)所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5 、2、3,则最大正方形E的面积是
、2、3,则最大正方形E的面积是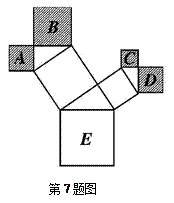
A. 13 B. 26 C. 47 D. 94
在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法中不正确的是( )
A.当 时,点B在⊙A内 时,点B在⊙A内 |
B.当 时,点B在⊙A内 时,点B在⊙A内 |
C.当 时,点B在⊙A外 时,点B在⊙A外 |
D.当 时,点B在⊙A外 时,点B在⊙A外 |
如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. |
B. |
C. |
D.2 |
. 已知二次函数 的图象如图所示,有下列四个结论:
的图象如图所示,有下列四个结论:
①b<0;②c>0;③b2-4ac>0;④a-b+c<0,其中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
在综合实践课上,六名同学做的作品的数量(单位:件)分别是:5,7,3,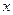 ,6,4;若这组数据的平均数是5,则这组数据的方差是 .
,6,4;若这组数据的平均数是5,则这组数据的方差是 .
如图,一次函数y=mx与反比例函数y= 的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若
的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若 =3,则k的值是 .
=3,则k的值是 .
如图所示,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度i=1∶0.5,则山的高度为____________米.
如图所示,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE. 求证:△ABE∽△ADC .
在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).
⑴小明的这三件文具中,可以看做是轴对称图形的是___________(填字母代号);
⑵小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?
2008年北京奥运会全球共选拔21880名火炬手,创历史记录.将这个数据精确到千位,用科学记数法表示为
A. |
B.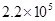 |
C.2.2×104 | D.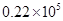 |
某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是
| A.众数是80 | B.中位数是75 | C.平均数是80 | D.极差是15 |
今年财政部将证券交易印花税税率由3‰调整为1‰(1‰表示千分之一).某人在调整后购买100000元股票,则比调整前少交证券交易印花税多少元?
| A.200元 | B.2000元 | C.100元 | D.1000元 |
下列命题中错误的是
| A.平行四边形的对边相等 | B.两组对边分别相等的四边形是平行四边形 |
| C.矩形的对角线相等 | D.对角线相等的四边形是矩形 |
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是
| A.y=(x-1)2+2 | B. |
C. |
D. |
如图2,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于
A. B.
B. C.
C. D.
D.
有5张质地相同的卡片,它们的背面都相同,正面分别印有“贝贝”、“晶晶”、“欢欢”、“迎迎”、“妮妮”五种不同形象的福娃图片.现将它们背面朝上,卡片洗匀后,任抽一张是“欢欢”的概率是
如图,直线OA与反比例函数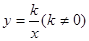 的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=
的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=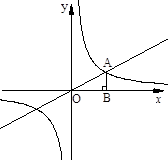
要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?小聪根据实际情况,以街道旁为x轴,建立了如图4所示的平面直角坐标系,测得A点的坐标为(0,3),B点的坐标为(6,5),则从A、B两点到奶站距离之和的最小值是 
如图5,在梯形ABCD中,AB∥DC, DB平分∠ADC,过点A作AE∥BD,交CD的
延长线于点E,且∠C=2∠E.
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图6和图7所示的统计图.根据图中信息解答下列问题:

(1)哪一种品牌粽子的销售量最大?
(2)补全图6中的条形统计图.
(3)写出A品牌粽子在图7中所对应的圆心角的度数.
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?
请你提一条合理化的建议.
如图8,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA= ,求△ACF的面积.
,求△ACF的面积.
“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
如图9,在平面直角坐标系中,二次函数 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=

(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.


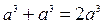
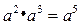
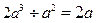

 与
与 轴交于点
轴交于点 ,关于
,关于 的解集是( )
的解集是( )






 =_____________________.
=_____________________.



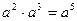
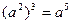
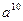 ÷
÷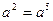





 ÷
÷ ,然后选取一个合适的a值,代入求值
,然后选取一个合适的a值,代入求值 粤公网安备 44130202000953号
粤公网安备 44130202000953号