如图，直线
分别与x轴、y轴交于A、B两点；直线
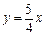与AB交于点C，与过点A且平行于y轴的直线交于点D.点E从点A出发，以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位
），点E的运动时间为t（秒）.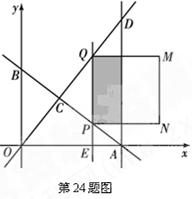
⑴求点C的坐标.
⑵当0<t<5时，求S与t之间的函数关系式.
⑶求⑵中S的最大值.
⑷当t>0时，直接写出点（4，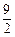
）在正方形PQMN内部时t的取值范围.
相关试题
＝ ，m＝ ，n＝ ；
的值．在某次抗险救灾中，消防官兵的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：
+12，﹣9，+8，﹣7，+11，﹣6，+10，﹣5．
（1）B地在A地什么方向，距离A地多少千米？
（2）若冲锋舟每千米耗油0．5升，油箱容量为30升，求途中还需补充多少升油．
，
，
，0，
，
，其中
，b＝2．
相关知识点
推荐套卷
粤公网安备 44130202000953号