如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是线段BC上一点,以AE为边在直线MN的上方作正方形AEFG

连结GD,求证△ADG≌△ABE;
如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=1,BC=2,E是线段BC上一动点(不含端点B,C ),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当E由B向C运动时,∠FCN的大小是否保持不变,若∠FCN的大小不变,求tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
相关知识点
推荐套卷
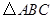 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).
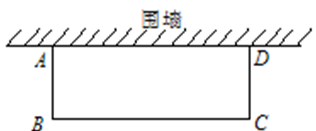
 ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.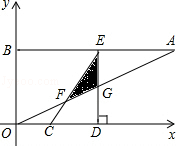
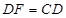 ?
?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号