海南省海口市初二上学期期末考试数学卷
如图,P为正方形ABCD内一点,将△ APB绕点B按逆时针方向旋转90°
APB绕点B按逆时针方向旋转90°
得到△BP′M,其中P与P′是对应点。
(1)作出旋转后的图形;
(2)若BP=5cm,试求△BPP′的周长和面积
如图所示,在⊙O中,AB是直径,CD是弦,AB⊥CD。
(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论。
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交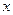 轴于D点,过点D作DF⊥AE于点F。
轴于D点,过点D作DF⊥AE于点F。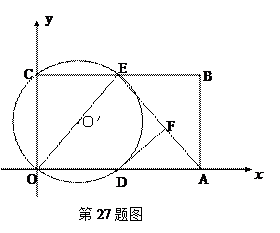
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形。由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”。你同意他的看法吗?请充分说明理由。
已知点(-2,y1),(-1,y2),(1,y3)都在直线y=- x+b上,则y1,y2,y3的值的大小关系是( ).
x+b上,则y1,y2,y3的值的大小关系是( ).
| A.y1>y2>y3 | B.y1<y2<y3 | C.y3>y1>y2 | D.y3>y1>y2 |
下列说法中正确的是…………………………………………… ( )
A.实数 是负数 是负数 |
B. |
C. 一定是正数 一定是正数 |
D.实数 的绝对值是 的绝对值是 |
若 ,则实数a在数轴上的对应点一定在………………… ( )
,则实数a在数轴上的对应点一定在………………… ( )
| A.原点左侧 | B.原点右侧 | C.原点或原点左侧 | D.原点或原点右侧 |
如图:D、E是△ABC的边AC、BC上的点,△ADB≌△EDB≌△EDC,下列结论:①AD=ED;②BC=2AB;③∠1=∠2=∠3;④∠4=∠5=∠6.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是
| A.1 号袋 | B.2 号袋 | C.3 号袋 | D.4 号袋 |
打开某洗衣机开关,在(洗衣机内无水)洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )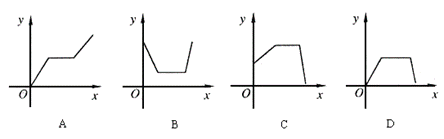
下列说法正确的是……………………( )
A. 的立方根是0.4 的立方根是0.4 |
B. 的平方根是 的平方根是 |
C.16的立方根是 |
D.0.01的立方根是0.000001 |
如图,已知直线 ,直线
,直线 ,直线
,直线 、
、 分别交x轴于B、C两点,
分别交x轴于B、C两点, 、
、 相交于点A。
相交于点A。
(1) 求A、B、C三点坐标;
(2) 求△ABC的面积。
下列计算正确的是
A.a+2 a2="3a3" a2="3a3" |
B.a3·a2="a6" | C.(a3)2="a6" | D.a8-a5=a3 |
以下列线段a、b、c的长为边,能构成直角三角形的是
| A.a="3," b="4," c=6 | B.a="1," b= , c= , c= |
| C.a="5," b="6," c=8 | D.a= ,b=2,c= ,b=2,c= |
如图2,点A、D、B、E在同一直线上,△ABC≌△DEF,AB=6,AE=10,则DB等于
A.2 B.2.5 C.3 D.4
如图2,点A、D、B、E在同一直线上,△ABC≌△DEF,AB=6,AE=10,则DB等于
A.2 B.2.5 C.3 D.4
如图3,□ABCD的对角线AC、BD相交于 点O,则图中的全等三角形共有
点O,则图中的全等三角形共有
A. 1对 B. 2对 C. 3对 D. 4对
如图4,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1等于 
| A.100° | B.110° | C.120° | D.130° |
如图5,在梯形ABCD中,AB∥DC,DE∥CB,△ADE周长为18,DC=4,则该梯形的周长为
| A.22 | B.26 | C.28 | D.30 |
一块边长为a米的正方形广场,扩建后的正方形边长比原来长2米,则扩建后广场面积增大了
| A.(4a+4)米2 | B.(a2+4)米2 | C.(2a+4)米2 | D.4米2 |
如图8,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(2a+b) ,宽为(a+b)的长方形,则需要C类卡片 张
如图9,在正方形网格中每个小正方形的边长都是单位1,已知△ABC和△A1B1C1关于点O成中心对称,点O直线x上.
(1)在图中标出对称中心O的位置;
(2)画出△A1B1C1关于直线x对称的△A2B2C2;
(3)△ABC与△A2B2C2满足什么几何变换?
如图10,在梯形ABCD中,AD∥BC,AB = DC=1,BD平分∠ABC,BD⊥CD.
= DC=1,BD平分∠ABC,BD⊥CD.
(1)求:① ∠BAD的度数;② BD的长;
(2)延长BC至点E,使C E=CD,说明△DBE是等腰三角形
E=CD,说明△DBE是等腰三角形
 的图象不经过第二象限,则k 的取值范围是( )
的图象不经过第二象限,则k 的取值范围是( )



 的图象不经过( )
的图象不经过( )
 ,则
,则 =
=  ,则
,则 =
=  和
和 ,则这个数为
,则这个数为  中自变量x的取值范围是_______
中自变量x的取值范围是_______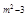 是正比例函数,则m=
是正比例函数,则m= 

 、
、 是实数,且
是实数,且 .解关于x的方程:
.解关于x的方程:
 所对应的点.(要求保留作图痕迹)
所对应的点.(要求保留作图痕迹)

 最接近的数是
最接近的数是


 ,b=
,b=

 粤公网安备 44130202000953号
粤公网安备 44130202000953号