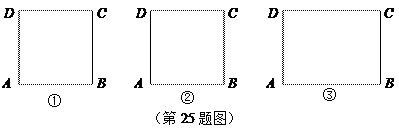初中数学圆解答题

如图，在□ABCD中，BE⊥AD于点E，BF⊥CD于点F，AC与BE、BF分别交于点G，H。

（1）求证：△BAE∽△BCF
（2）若BG＝BH，求证四边形ABCD是菱形

如图：把一张给定大小的长方形卡片ABCD放在宽度为10mm的横格纸中，恰好四个顶点都在横格线上，已知α＝32°，求长方形卡片的周长。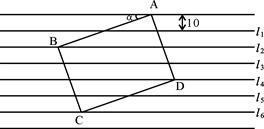

（参考数据  sin32°≈0.5        cos32°≈0.8        tan32°≈0.6）

(本小题满分8分)
如图所示，某幼儿园有一道长为16米的墙，计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD．求该矩形草坪BC边的长．

已知：如图，E，F分别是ABCD的边AD，BC的中点．求证：AF=CE．

如图，在□ABCD中，点E、F是对角线AC上两点，且AE=CF．

求证：∠EBF=∠FDE．

（本小题满分8分）
　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；
（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

如图，在梯形ABCD中，AB∥CD
（1）用尺规作图方法，作∠DAB的角平分线AF（只保留作图痕迹，不写作法和证明）
（2）若AF交CD边于点E，判断△ADE的形状（只写结果）

如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.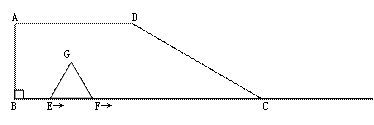

⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；
⑵若△EFG与梯形ABCD重叠部分面积是y，求
①当0＜x≤2时，y与x之间的函数关系式；
②当2＜x≤6时，y与x之间的函数关系式；
⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.

．(10分)如图9，正方形ABCD边长为10cm，P、Q分别是BC、CD上的两个动点，当P 点在BC上运动时，且A P⊥PQ.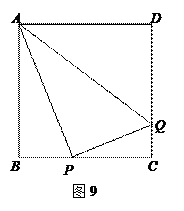

（1）求证：△ABP∽△PCQ；
（2）当BP等于多少时，四边形ABCQ的面积为62cm²．

如图7，一个农户用24m长的篱笆围成一排一面靠墙、大小相等且彼此相连的三个矩形鸡舍.

要使这三个鸡舍的总面积为36m²，求每个鸡舍的长和宽各是多少.

问题探究
（1）请在图①的正方形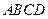内，画出使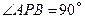的一个点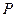，并说明理由．
（2）请在图②的正方形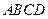内（含边），画出使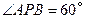的所有的点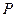，并说明理由．
问题解决
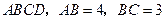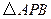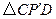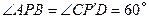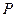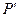（3）如图③，现在一块矩形钢板．工人师傅想用它裁出两块全等的、面积最大的和钢板，且．请你在图③中画出符合要求的点和，并求出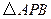的面积（结果保留根号）．

如图，在中，点是的中点，连接并延长，交的延长线于点F．

求证：．

（本小题满分7分）
如图，矩形ABCD，AB＝4，AD＝3，动点M、N分别从D、B同时出发，以1个
单位/秒的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动。过点
N作NP⊥BC，交AC于点P，连结MP。已知动点M、N运动了秒．
⑴请直接写出PN的长；（用含的代数式表示）
⑵若0秒≤≤1秒，试求△MPA的面积S与时间秒的函数关系式，利用函数图
象，求S的最大值；
⑶若0秒≤≤3秒，△MPA能否为一个等腰三角形？若能，试求出所有的对应
值；若不能，试说明理由．