2010年高级中等学校招生考试数学卷(广东珠海)
如图1,抛物线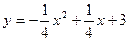 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线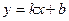 交于A、D两点。
交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?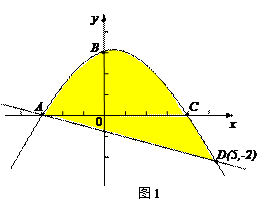

如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.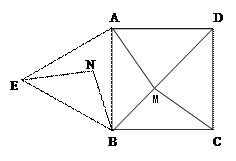
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为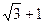 时,求正方形的边长.
时,求正方形的边长.
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).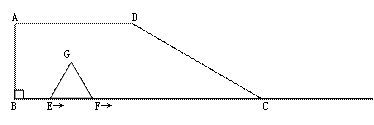
⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
如图1,
在△ABC中,D是BC延长线上一点, ∠B = 40°,∠ACD = 120°,则∠A等于
| A.60° | B.70° | C.80°3 | D.90° |
如图2,在□ABCD中,AC平分∠DAB,AB = 3, 则□ABCD的周长为
| A.6 | B.9 | C.12 | D.15 |
如图3,
在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是
| A.点P | B.点Q | C.点R | D.点M |
小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是
A. |
B. |
C. |
D. |
一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是
如图4,
两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是
| A.7 | B.8 | C.9 | D.10 |
如图5,
已知抛物线 的对称轴为
的对称轴为 ,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
| A.(2,3) | B.(3,2) | C.(3,3) | D.(4,3) |
将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图6-1.在图6-2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图6-1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是
| A.6 | B.5 | C.3 | D.2 |
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从图8的四张卡片中任意拿走一张,使剩下的卡片从左到右连成一个三位数,该数就是他猜的价格.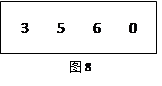
若商品的价格是360元,那么他一次就能猜中的概率是 .
某盏路灯照射的空间可以看成如图9所示的圆锥,它的高AO = 8米,母线AB与底面半径OB的夹角为 ,
, ,则圆锥的底面积是 平方米(结果保留π).
,则圆锥的底面积是 平方米(结果保留π).
把三张大小相同的正方形卡片A,B,C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.
若按图10-1摆放时,阴影部分的面积为S1;若按图10-2摆放时,阴影部分的面积为S2,则S1S2(填“>”、“<”或“=”).
某校乒乓球训练队共有9名队员,他们的年龄(单位:岁)分别为:12,13,13,14,12,13,15,13,15,则他们年龄的众数为( )
| A.12 | B.13 | C.14 | D.15 |
在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是( )
| A.(-2,6) | B.(-2,0) | C.(-5,3) | D.(1,3) |
如图,PA、PB是O的切线,切点分别是A、B,如果∠P=60°,
那么∠AOB等于( )
A.60° B.90° C.120° D.150°
一天,小青在校园内发现:旁边一颗树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).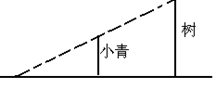
如果小青的峰高为1.65米,由此可推断出树高是_______米.
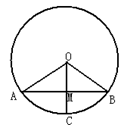
如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,
则点P到BC的距离是_____cm.
我们常用的数是十进制数,计算机程序使用的是二进制数
(只有数码0和1),它们两者之间可以互相换算,如将(101)2,
(1011)2换算成十进制数应为:

按此方式,将二进制(1001)2换算成十进制数的结果是_______________.
如图,在梯形ABCD中,AB∥CD
(1)用尺规作图方法,作∠DAB的角平分线AF(只保留作图痕迹,不写作法和证明)
(2)若AF交CD边于点E,判断△ADE的形状(只写结果)
2010年亚运会即将在广州举行,广元小学开展了“你最喜欢收看的亚运五项球比赛(只选一项)”抽样调查.根据调查数据,小红计算出喜欢收看排球比赛的人数占抽样人数的6%,小明则绘制成如下不完整的条形统计图,请你根据这两位同学提供的信息,解答下面的问题:
(1)将统计补充完整;
(2)根据以上调查,试估计该校1800名学生中,最喜欢收看羽毛球的人数.
已知:正比例函数y=k1x的图象与反比例函数 (x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),
(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),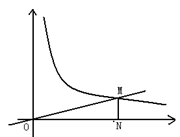
若△OMN的面积等于2,求这两个函数的解析式.
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
中央电视台举办的第14届“蓝色经典·天之蓝”杯青年歌手大奖赛,由部队文工团的A(海政)、B(空政)、C(武警)组成种子队,由部队文工团的D(解放军)和地方文工团的E(云南)、F(新疆)组成非种子队.现从种子队A、B、C与非种子队D、E、F中各抽取一个队进行首场比赛.
(1)请用适当方式写出首场比赛出场的两个队的所有可能情况(用代码A、B、C、D、E、F表示);
(2)求首场比赛出场的两个队都是部队文工团的概率P.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.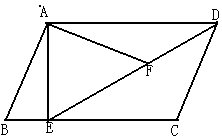
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3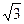 ,AE=3,求AF的长.
,AE=3,求AF的长.
今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少?
如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连结P
| A.P | B.P | C.P | D.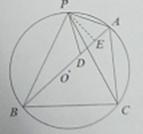 (1)当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并证明; (2)若cos∠PCB= 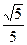 ,求PA的长. ,求PA的长. |
如图,平面直角坐标系中有一矩形ABCD(O为原点),点A、C分别在x轴、y轴上,且C点坐标为(0,6);将BCD沿BD折叠(D点在OC边上),使C点落在OA边的E点上,并将BAE沿BE折叠,恰好使点A落在BD的点F上.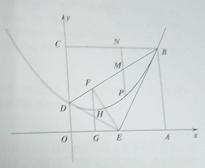
(1)直接写出∠ABE、∠CBD的度数,并求折痕BD所在直线的函数解析式;
(2)过F点作FG⊥x轴,垂足为G,FG的中点为H,若抛物线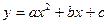 经过B、H、D三点,求抛物线的函数解析式;
经过B、H、D三点,求抛物线的函数解析式;
(3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PM<NM、PM=MN、PM>MN成立的x的取值范围。
 2) 的结果是
2) 的结果是



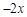 < 4的解集表示在数轴上,正确的是
< 4的解集表示在数轴上,正确的是
 的结果是
的结果是


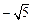 的相反数是 .
的相反数是 .
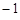 ,则点B所对应的数为 .
,则点B所对应的数为 . 的一个根,则
的一个根,则 的值为 .
的值为 .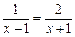 .
.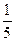
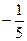

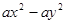 =________________.
=________________. 
 的解是__________.
的解是__________.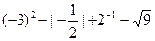
 的一个根,求m的值及方程的另一根x2。
的一个根,求m的值及方程的另一根x2。 粤公网安备 44130202000953号
粤公网安备 44130202000953号