2010年高级中等学校招生考试数学卷(福建宁德)
2007年中国月球探测工程的“嫦娥一号”卫星将发射升空飞向月球. 已知地球距离月球表面约为384000千米,那么这个距离用科学记数法(保留三个有效数字)表示应为( )
A. 千米 千米 |
B. 千米 千米 |
C. 千米 千米 |
D. 千米 千米 |
一列数:0,1,2,3,6,7,14,15,30,____,____,____,____这串数是由小新按照一定规则写下来的,他第一次写下“0,1”,第二次接着写“2,3”,第三次接着写“6,7”,第四次接着写“14,15”,就这样一直接着往下写,那么这列数的后面三个数应该是下面的( )
| A.31,32,64 | B.31,32,33 | C.31,62,63 | D.31,45,46 |
某单位需以“挂号信”或“特殊快递”的方式向五所学校各寄一封信.这五封信的质量分别是90g,72g,215g,340g,400g. 根据这五所学校的地址及信件的质量范围,在邮局查得相关邮费标准如下:
| 业务种类 |
计费单位 |
资费标准 (元) |
挂号费 (元/封) |
特制信封 (元/个) |
| 挂号信 |
首重100g内,每20g |
0.8 |
3.0 |
0.5 |
| 续重101g—2000g 每100g |
2.0 |
|||
| 特快专递 |
首重1000g (含1000g) |
5.0 |
3.0 |
1.0 |
|
(1) 质量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2) 这五封信分别以怎样的方式寄出最合算?请说明理由.
下列事件是必然事件的是( ).
| A.随意掷两个均匀的骰子,朝上面的点数之和为6 |
| B.抛一枚硬币,正面朝上 |
| C.3个人分成两组,一定有2个人分在一组 |
| D.打开电视,正在播放动画片 |
如图,
在⊙O中,∠ACB=34°,则∠AOB的度数是( ).
| A.17° | B.34° | C.56° | D.68° |
今年颁布的《国家中长期教育改革和发展规划纲要》中指出,“加大教育投入.提高国家财政性教育经费支出占国内生产总值比例,2012年达到4%.”如果2012年我国国内生产总值为435000亿元,那么2012年国家财政性教育经费支出应为(结果用科学记数法表示)( ).
| A.4.35×105亿元 | B.1.74×105亿元 | C.1.74×104亿元 | D.174×102亿元 |
反比例函数 (x>0)的图象如图所示,
(x>0)的图象如图所示,
随着x值的增大,y值( ).
| A.减小 | B.增大 | C.不变 | D.先减小后不变 |
如图,在8×4的方格(每个方格的边长为1个单位长)中,
⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( ).
| A.内含 | B.内切 | C.相交 | D.外切 |
如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个
直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ).

A.2+ |
B.2+2 |
C.12 | D.18 |
下表是中国2010年上海世博会官方网站公布的5月某一周入园参观人数,
则这一周入园参观人数的平均数是__________万.
| 日期 |
22日 |
23日 |
24日 |
25日 |
26日 |
27日 |
28日 |
| 入园人数(万) |
36.12 |
31.14 |
31.4 |
34.42 |
35.26 |
37.7 |
38.12 |
如图,
在直径AB=12的⊙O中,弦CD⊥AB于M,且M是半径OB的中点,
则弦CD的长是_______(结果保留根号).
用m根火柴可以拼成如图1所示的x个正方形,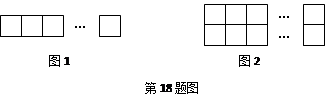
还可以拼成如图2所示的2y个正方形,那么用含x的代数式表示y,得y=_____________.
(每小题7分,满分14分)
⑴ 化简:(a+2)(a-2)-a(a+1);
⑵ 解不等式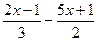 ≤1,并把它的解集在数轴上表示出来.
≤1,并把它的解集在数轴上表示出来.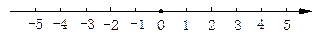
本题满分8分)如图,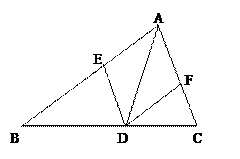
已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明.
某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

⑴ 九年级(1)班参加体育测试的学生有_________人;
⑵ 将条形统计图补充完整;
⑶ 在扇形统计图中,等级B部分所占的百分比是___,等级C对应的圆心角的度数为___°;
⑷ 若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有___人.
我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,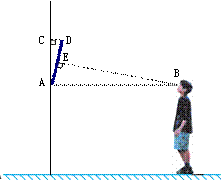
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).
据宁德网报道:第三届海峡两岸茶业博览会在宁德市的成功举办,提升了闽东茶叶的国内外知名度和市场竞争力,今年第一季茶青(刚采摘下的茶叶)每千克的价格是去年同期价格的10倍.茶农叶亮亮今年种植的茶树受霜冻影响,第一季茶青产量为198.6千克,比去年同期减少了87.4千克,但销售收入却比去年同期增加8500元.求茶农叶亮亮今年第一季茶青的销售收入为多少元?
如图1,抛物线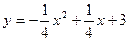 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线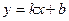 交于A、D两点。
交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?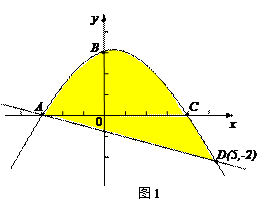

如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.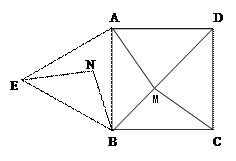
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为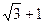 时,求正方形的边长.
时,求正方形的边长.
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).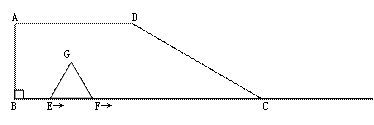
⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
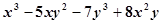 按某一个字母的升幂排列,正确的是( )
按某一个字母的升幂排列,正确的是( )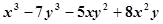
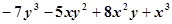
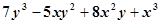
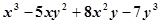
 ,那么
,那么 等于( )
等于( ) <3时,化简
<3时,化简 的结果是( )
的结果是( )

 的相反数是__________
的相反数是__________ 的系数是_________
的系数是_________ 与
与 互为相反数,则
互为相反数,则 ________
________ 去括号后的结果是___________
去括号后的结果是___________ ,-1,
,-1, ,
, ,
, 中,是整式的有______个.
中,是整式的有______个. ,
, ,
, ,
, 这四个数中,最大的数与最小的数的和等于______
这四个数中,最大的数与最小的数的和等于______ ________时,
________时, 与
与 的和是单项式
的和是单项式 的最大值是_____________
的最大值是_____________

 [
[ ]
] 



 ,其中
,其中 ,
,
 ,其中
,其中 ,
,
 、
、 、
、 在数轴上的位置如图所示,
在数轴上的位置如图所示,

 的倒数是 ;
的倒数是 ;  的相反数是 .
的相反数是 . = ;
= ;  .
.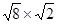 = ;
= ; 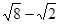 = .
= .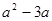 = ; 化简:
= ; 化简: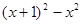 = .
= . 的相反数是( ).
的相反数是( ).






 _____________.
_____________.
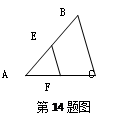
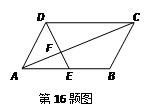
 粤公网安备 44130202000953号
粤公网安备 44130202000953号