2010年高级中等学校招生全国统一考试数学卷(江苏镇江)
若正比例函数的图象经过点( ,2),则这个图象必经过点( ).
,2),则这个图象必经过点( ).
| A.(1,2) | B.( , , ) ) |
C.(2, ) ) |
D.(1, ) ) |
若用半径为9,圆心角为 的扇形围成一个圆锥的侧面
的扇形围成一个圆锥的侧面 (接缝忽略不计),则这个圆锥的底面半径是( ).
(接缝忽略不计),则这个圆锥的底面半径是( ).
| A.1.5 | B.2 | C.3 | D.6 |
如图,
 ,
, 可以看作是由
可以看作是由 绕点
绕点 顺时针旋转
顺时针旋转 角度得到的.若点
角度得到的.若点 在
在 上,则旋转角
上,则旋转角 的大小可以是( ).
的大小可以是( ).
A. |
B. |
C. |
D. |
根据下表中的二次函数 的自变量
的自变量 与函数
与函数 的对应值,可判断该二次函数的图象与
的对应值,可判断该二次函数的图象与 轴( ).
轴( ).
 |
… |
 |
 |
 |
 |
… |
||||
 |
… |
 |
 |
 |
 |
…
|
一家商店将某种商品按成本价提高50%后,标价为450元,又以8折出售,则售出这件商品可获利润__________元.
某校为了组织一项球类对抗赛,在本校随机调查了若干名学生,对他们每人最喜欢的一项球类运动进行了统计,并绘制成如图①、②所示的条形和扇形统计图.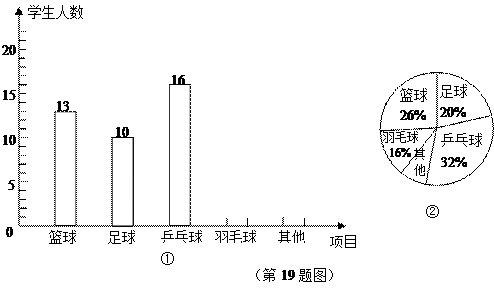
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数,并补全条形统计图;
(2)若全校有1 500名学生,请你估计该校最喜欢篮球运动的学生人数;
(3)根据调查结果,请你为学校即将组织的一项球类对抗赛提出一条合理化建议.
小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点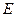 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度
处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度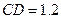 m,
m,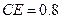 m,
m,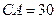 m(点
m(点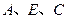 在同一直线上).
在同一直线上).
已知小明的身高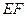 是1.7m,请你帮小明求出楼高
是1.7m,请你帮小明求出楼高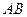 (结果精确到0.1m).
(结果精确到0.1m).
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发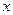 (h)时,汽车与甲地的距离为
(h)时,汽车与甲地的距离为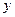 (km),
(km),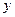 与
与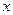 的函数关系如图所示.
的函数关系如图所示.
根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中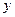 与
与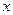 之间的函数表达式;
之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.
如图,在平面直角坐标系中,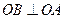 ,且
,且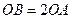 ,点
,点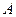 的坐标是
的坐标是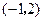 .
.
(1)求点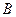 的坐标;
的坐标;
(2)求过点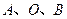 的抛物线的表达式;
的抛物线的表达式;
(3)连接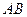 ,在(2)中的抛物线上求出点
,在(2)中的抛物线上求出点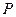 ,使得
,使得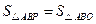 .
.
问题探究
(1)请在图①的正方形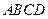 内,画出使
内,画出使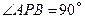 的一个点
的一个点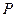 ,并说明理由.
,并说明理由.
(2)请在图②的正方形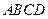 内(含边),画出使
内(含边),画出使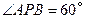 的所有的点
的所有的点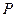 ,并说明理由.
,并说明理由.
问题解决
(3)如图③,现在一块矩形钢板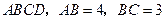 .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的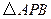 和
和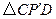 钢板,且
钢板,且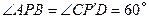 .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点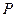 和
和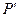 ,并求出
,并求出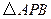 的面积(结果保留根号).
的面积(结果保留根号).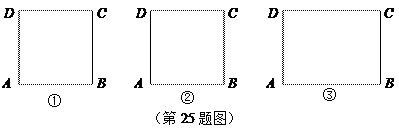
反比例函数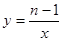 的图象在第二、四象限,则n的取值范围为 ,
的图象在第二、四象限,则n的取值范围为 ,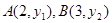 为图象上两点,则y1 y2(用“<”或“>”填空)
为图象上两点,则y1 y2(用“<”或“>”填空)
如图,在平行四边形ABCD中,CD=10,F是AB边上一点,DF交AC于点E,
且 = ,BF= .
= ,BF= .
有A,B两只不透明口袋,每只品袋里装有两只相同的球,A袋中的两只球上分别写了“细”、“致”的字样,B袋中的两只球上分别写了“信”、“心”的字样,从每只口袋里各摸出一只球,刚好能组成“细心”字样的概率是 ( )
A. |
B. |
C. |
D. |
已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于 ( )
A.8 |
B.9 |
C.10 |
D.11 |
两直线 的交点坐标为 ( )
的交点坐标为 ( )
| A.(—2,3) | B.(2,—3) | C.(—2,—3) | D.(2,3) |
小明新买了一辆“和谐”牌自行车,说明书中关于轮胎的使用说明如下:
小明看了说明书后,和爸爸讨论:小明经过计算,得出这对轮胎能行驶的最长路程是( )
| A.9.5千公里 | B. 千公里 千公里 |
C.9.9千公里 | D.10千公里 |
推理证明(本小题满分6分)
如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求旋转角的大小.
(本小题满分6分)
在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
(1)作出△ABC关于y轴对称的△A1B1C1,其中A,B,C分别和A1,B1,C1对应;
(2)平移△ABC,使得A点在x轴上,B点在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中A,B,C分别和A2,B2,C2对应;
(3)填空:在(2)中,设原△ABC的外心为M,△A2B2C2的外心为M,则M与M2之间的距离为 .
在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于A,B两点.
(1)求直线l的函数关系式;
(2)求△AOB的面积.
已知二次函数 的图象C1与x轴有且只有一个公共点.
的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(—3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
(3)若 的取值范围.
的取值范围.
实践应用(本小题满分6分)
有200名待业人员参加某企业甲、乙、丙三个部门的招聘,到各部门报名的人数百分比见图表1,该企业各部门的录取率见图表2.(部门录取率= ×100%)
×100%)
(1)到乙部门报名的人数有 人,乙部门的录取人数是 人,该企业的录取率为 ;
(2)如果到甲部门报名的人员中有一些人员改到丙部门报名,在保持各部门录取率不变的情况下,该企业的录取率将恰好增加15%,问有多少人从甲部门改到丙部门报名?
海宝在研究数学问题时发现了一个有趣的现象:
(1)请你用数学表达式补充完整海宝发现的这个有趣的现象;
(2)请你证明海宝发现的这个有趣现象.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=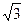 ,∠ACB=30°.
,∠ACB=30°.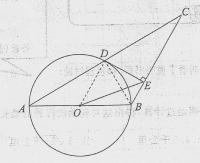
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
如图,在直角坐标系 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,

试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
 在第四象限,那么m的取值范围是( ).
在第四象限,那么m的取值范围是( ).



 的结果是( ).
的结果是( ).



 =__________.
=__________.
 ,直线
,直线 分别交
分别交 于点
于点 ,
, ,则
,则 的大小是__________.
的大小是__________. 是双曲线
是双曲线 上的两点,且
上的两点,且 ,则
,则 {填“>”、“=”、“<”}.
{填“>”、“=”、“<”}.
 中,
中, ,
, .若
.若 ,
, ,则这个梯形的面积是__________.
,则这个梯形的面积是__________.
 中,
中, ,
, 的平分线交
的平分线交 于点
于点 分别是
分别是 和
和 上的动点,则
上的动点,则 的最小值是___________ .
的最小值是___________ .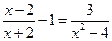 .
. 中,点
中,点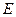 是
是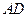 的中点,连接
的中点,连接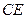 并延长,交
并延长,交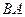 的延长线于点F.
的延长线于点F.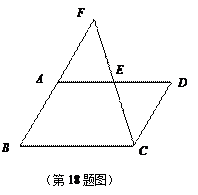
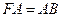 .
.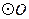 是
是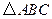 的外接圆,
的外接圆,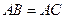 ,过点
,过点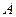 作
作 ,交
,交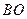 的延长线于点
的延长线于点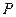 .
.
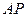 是
是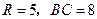 ,求线段
,求线段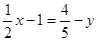
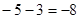

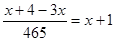
 +1<8的最大整数解是( )
+1<8的最大整数解是( ) 的方程
的方程 的解满足方程
的解满足方程 ,则
,则 的值为( )
的值为( )

 ,那么
,那么 .
. ,那么
,那么 .
. ,那么
,那么 .
. ,那么
,那么 .
. 中的分母化为整数,正确的是( )
中的分母化为整数,正确的是( )



 、那么a的值是( )
、那么a的值是( ) 的倒数是 ;
的倒数是 ;  的相反数是 .
的相反数是 . = ;
= ;  .
.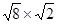 = ;
= ; 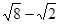 = .
= .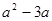 = ; 化简:
= ; 化简: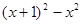 = .
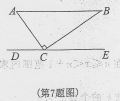
= .
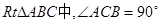 ,DE过点C,且DE//AB,若
,DE过点C,且DE//AB,若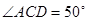 ,
,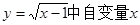 的取值范围是 ,当
的取值范围是 ,当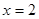 时,函数值y= .
时,函数值y= .
 的最大值为 .
的最大值为 .
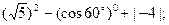
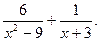




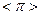 = (
= ( 为圆周率);
为圆周率); 的取值范围为 ;
的取值范围为 ; ;
; 不恒成立;
不恒成立; 的值;
的值; 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为 的个数记为b.
的个数记为b.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号