(本小题满分6分)
在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
(1)作出△ABC关于y轴对称的△A1B1C1,其中A,B,C分别和A1,B1,C1对应;
(2)平移△ABC,使得A点在x轴上,B点在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中A,B,C分别和A2,B2,C2对应;
(3)填空:在(2)中,设原△ABC的外心为M,△A2B2C2的外心为M,则M与M2之间的距离为 .
相关知识点
推荐套卷

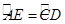 ,连接CE,M是CE的中点,延长DE到点G,使得EG=DE,并且交AF的延长线于点G,此时F恰为AG的中点.
,连接CE,M是CE的中点,延长DE到点G,使得EG=DE,并且交AF的延长线于点G,此时F恰为AG的中点.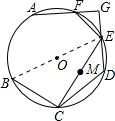
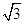 ,求⊙O的周长.
,求⊙O的周长.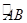 上是否存在一点N,使得四边形NMEF是轴对称图形,并说明理由.
上是否存在一点N,使得四边形NMEF是轴对称图形,并说明理由.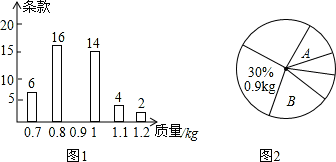
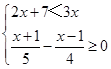 .
.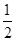 nx成正比,在试行过程中得到了如下两组数据:①工作12年的员工,若其工作数量为50单位,则其工作业绩为3700元;②工作16年的员工,若其工作数量为80单位,则其工作业绩为6320元.
nx成正比,在试行过程中得到了如下两组数据:①工作12年的员工,若其工作数量为50单位,则其工作业绩为3700元;②工作16年的员工,若其工作数量为80单位,则其工作业绩为6320元. 粤公网安备 44130202000953号
粤公网安备 44130202000953号