问题探究：
（1）请在图①中作出两条直线，使它们将圆面四等分；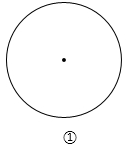
（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M）使它们将正方形ABCD的面积四等分，并说明理由．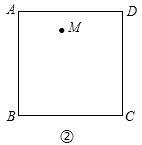
问题解决：
（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=a，CD=b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？如若存在，求出BQ的长；若不存在，说明理由．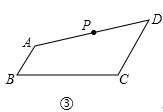
相关试题
△ABC中，∠C=90°，BC=6，AC=8，AB=10.求边AB上的高的长.
解：作CD⊥AB垂足为D.
△ABC把BC看作底，则_________是高.此时面积为_________=_________.
若把AB看作底，则_________是高，此时面积为_________.
∴_________=_________.∴CD=_________.
相关知识点
推荐套卷
粤公网安备 44130202000953号