如图，在直角坐标系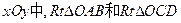
的直角顶点A，C始终在x轴的正半轴上，B，D在第一象限内，点B在直线OD上方，OC=CD，OD=2，M为OD的中点，AB与OD相交于E，当点B位置变化时，
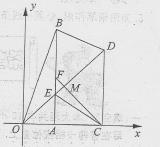
试解决下列问题：
（1）填空：点D坐标为 ；
（2）设点B横坐标为t，请把BD长表示成关于t的函数关系式，并化简；
（3）等式BO=BD能否成立？为什么？
（4）设CM与AB相交于F，当△BDE为直角三角形时，判断四边形BDCF的形状，并证明你的结论.
相关试题
小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元；如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？
，D、E分别是半径OA和OB的中点，试判断CD与CE的大小关系，并说明理由．
如图，四边形ABCD中，∠ABC=∠ADC=90°，BD⊥AC，垂足为P．
（1）请作出Rt△ABC的外接圆⊙O；（保留作图痕迹，不写作法）
（2）点D在⊙O上吗？说明理由；
（3）试说明：AC平分∠BAD．
如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C．若AB是⊙O的直径，D是BC的中点．
（1）试判断AB、AC之间的大小关系，并说明理由；
（2）在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点．（直接写出结论）
相关知识点
推荐套卷
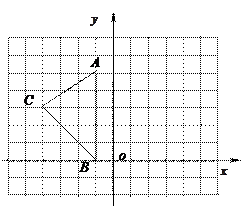
粤公网安备 44130202000953号