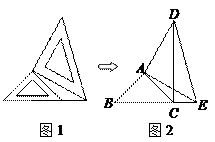
两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．请找出图2中的全等三角形，_____≌____并给予证明（说明：结论中不得含有未标识的字母）；
证明：DC⊥BE．
；
；
；
；
的式子表示出来；
，求
的最小值；
是正数，则
的最小值为。
，其中
，计算：
；（2）
；（2）
相关知识点
推荐套卷
两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．请找出图2中的全等三角形，_____≌____并给予证明（说明：结论中不得含有未标识的字母）；
证明：DC⊥BE．
粤公网安备 44130202000953号