北京市东城南区初二上学期期末考试数学卷
一次函数y=kx+b图象经过点(1,3)和(4,6) 。
。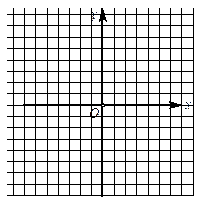
①试求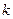 与
与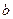 ;
;
② 画出这个一次函数图象;
画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y=0;
⑤当x 时,y﹥0;
如图,在□ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断线段BE、DF的关系,并证明你的结论
如图, 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系; 表示摩托车厂一天的销售成本与销售量的关系。(利润=收入-成本)
表示摩托车厂一天的销售成本与销售量的关系。(利润=收入-成本)
(1)写出销售收入与销售量之间的函数关系式: ,
(2)写出销售成本与销售量之间的函数关系式: ,
观察图像得:
(3)当一天的销售量为 辆时,销售收入等于销售成本;
(4)当一天的销售超过 辆时,工厂才能获利。
如图,在△ABC中,∠ACB= ,CD是斜边AB上的高,则图中相似三角形有( ▼ )
,CD是斜边AB上的高,则图中相似三角形有( ▼ )
| A.1对 | B.2对 | C.3对 | D.4对 |
在△ABC中,∠ACB= ,则
,则 表示的是( ▼ )
表示的是( ▼ )
| A.sinA | B.cosA | C.tanA | D.cotA |
如果 与
与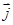 均是单位向量,以下关系式:(1)
均是单位向量,以下关系式:(1)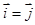 ,(2)
,(2)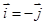 ,(3)
,(3)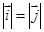 中,正确的有( ▼ )
中,正确的有( ▼ )
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西 方向航行,乙船沿南偏西
方向航行,乙船沿南偏西 方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的( ▼ )
方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的( ▼ )
A. 南偏西 B. 南偏西
B. 南偏西 C. 南偏西
C. 南偏西 D. 南偏西
D. 南偏西
已知D是△ABC边AB上的点,且△ABC的面积为2010,AD∶DB=3∶2,那么△ACD的面积是 ▼
如图,D、E、F是△ABC三边上的点,且DE‖BC,EF‖AB,DE∶BC=1∶3,那么EF∶AB= ▼ 
如图,D、E、F、G是△ABC边上的点,且DE‖FG‖BC,DE,FG将△ABC分成三个部分,它们的面积比为S1∶S2∶S3=1∶2∶3,那么DE∶FG∶BC = ▼ .
如图,某人在一个建筑物(AM)的顶部A观察另一个建筑物(BN)的顶部B的仰角为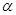 , 如果建筑物AM的高度为50米(即AM=50),两建筑物间的间距为60米(即MN=60),
, 如果建筑物AM的高度为50米(即AM=50),两建筑物间的间距为60米(即MN=60),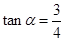 ,那么建筑物BN的高度为___▼ 米.
,那么建筑物BN的高度为___▼ 米.
如图,D是△ABC内一点,且∠ADC=∠BDA=∠BDC,如果AD=2,BD=3,∠ABC=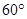 ,那么CD= ▼ .
,那么CD= ▼ .
“五一”长假小明和父母一起去云南旅游,他们到“野象谷”游玩是乘坐缆车进谷的,小明听导游说,这里的缆车单程长为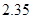 千米,在钢缆上来回均匀地安装着188个吊窗,并且这些吊窗按顺序编号:1,2,3,4,……,187,188.小明入谷时乘坐的是45号吊窗,途中他观察迎面而来的吊窗的编号,他先看到142号,过一会他又看到145号,那么当他和145号吊窗并排时,他离缆车终点还有约 ▼ 米.
千米,在钢缆上来回均匀地安装着188个吊窗,并且这些吊窗按顺序编号:1,2,3,4,……,187,188.小明入谷时乘坐的是45号吊窗,途中他观察迎面而来的吊窗的编号,他先看到142号,过一会他又看到145号,那么当他和145号吊窗并排时,他离缆车终点还有约 ▼ 米.
如图,在△ABC中,BC=9,AB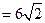 ,∠ABC=
,∠ABC=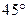 .
. 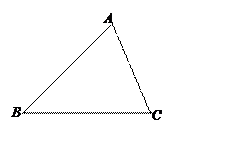
(1)求△ABC的面积;
(2)求cos∠C的值.
如图,梯形ABCD中,AB‖CD,且AB∶CD=4∶3,E是CD的中点,AC与BE交于点F. 
(1)求 的值;
的值;
(2)若 ,请用
,请用 来表示
来表示
如图,在△ABC中,∠ACB= ,D是AB延长线上一点,且BD=BC,CE⊥CD交AB于E.
,D是AB延长线上一点,且BD=BC,CE⊥CD交AB于E.
(1)求证:△ACE∽△ADC;
(2)若BE∶EA=3∶2,求sin∠A的值.
下列分解因式正确的是( )
A.x3–x="x(x2-1)"  |
B.m2+m-6=(m+3)(m-2) |
| C.a2-16=(a-4)2 | D.x2+y2=(x+y)(x-y) |
判断下列的哪个点是在函数 的图象上 ( )
的图象上 ( )
| A.(-2.5,-4) | B.(1,3) | C.(2.5,4) | D.(2,1) |
如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为( )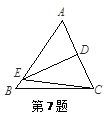
| A.16cm | B.28cm | C.26cm | D.18cm |
如图,E、B、F、C四点在一条直线上,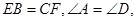 再添一个条件仍不能证明△ABC≌△DEG的是( )
再添一个条件仍不能证明△ABC≌△DEG的是( )
A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE
如图1,长方形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为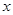 ,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )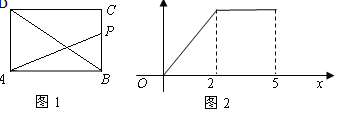
| A.3 | B.4 | C.5 | D.6 |
如果一次函数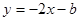 的图象经过点A(1,-1),那么
的图象经过点A(1,-1),那么 ____,该函数图象与
____,该函数图象与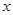 轴的交点坐标是_____,与
轴的交点坐标是_____,与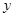 轴的交点坐标是_____
轴的交点坐标是_____
已知一次函数的图象经过(0,2),且函数y的值随自变量x的增大而减小,请写出一个符合上述条件的一次函数的解析式是
如图,有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连结BC并延长到E,使CE=CB,连接DE,那么量出DE的长就等于AB的长,可根据 定理判定△ABC≌△DEC.
如图,有两个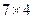 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求: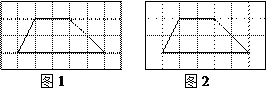
(1)线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论.
已知平面直角坐标系中有A(-2,1),B(2,3)两点.
(1)在x轴上找一点C,使CA+CB最小,并求出点C的坐标;
(2)在x轴上找一点D,使等△ABD为等腰三角形,并通过画图说明使△ABD为等腰三角形的点D有多少个.
仔细阅读下面例题,解答问题:
例题: 已知二次三项式 有一个因式是
有一个因式是 ,求另一个因式以及
,求另一个因式以及 的值.
的值.
解:设另一个因式为 ,得
,得

 .
.
则 .
.
∴ 
解得: .
.
∴ 另一个因式为 ,
, 的值为-21 .
的值为-21 .
问题:仿照以上方法解 答下面问题:
答下面问题:
已知二次三项式 有一个因式是
有一个因式是 ,求另一个因式以及
,求另一个因式以及 的值.
的值.
已知函数 和
和 .
.
(1)请在同一坐标系中画出这两个函数的图象;
(2)求出这两个函数图像 的交点坐标;
的交点坐标;
(3)观察图象,回答当x取何值时 .
.
康乐公司在 两地分别有同型号的机器
两地分别有同型号的机器 台和
台和 台,现要运往甲地
台,现要运往甲地 台,乙地
台,乙地 台,从
台,从 两地运往甲、乙两地的费用如下表:
两地运往甲、乙两地的费用如下表:
| |
甲地(元/台) |
乙地(元/台) |
| 地 |
 |
 |
| 地 |
 |
 |
(1)如果从地运往甲地 台,求完成以上调运所需总费用
台,求完成以上调运所需总费用 (元)与
(元)与 (台)之间的函数关系式;
(台)之间的函数关系式;
(2)请你为康乐公司设计一种最佳调运方案,使总费用最少,并说明理由
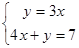

 (2)
(2)
 的图像如图所示,则下列关系式中错误的是( ▼ )
的图像如图所示,则下列关系式中错误的是( ▼ )




 ,
, 是方程
是方程 的两个实数根,那么
的两个实数根,那么 的值为( ▼ )
的值为( ▼ )



 的值为 ▼
的值为 ▼  ,那么CD的长是 ▼ .
,那么CD的长是 ▼ . 
 ,cosA=
,cosA= ,AB=6,那么AC= ▼
,AB=6,那么AC= ▼ 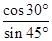 = ▼
= ▼ 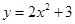 的图像向上平移2个单位,那么所得图像的函数解析式是 ▼
的图像向上平移2个单位,那么所得图像的函数解析式是 ▼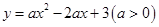 图像上点(2,n)与(3,m),则 n ▼ m. (填“>,<,或无法确定”)
图像上点(2,n)与(3,m),则 n ▼ m. (填“>,<,或无法确定”) 的图像经过点
的图像经过点 与
与 .
. 的平方根是( )
的平方根是( )







 )
)
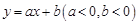 和
和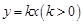 的图象交于点
的图象交于点 ,那么点
,那么点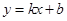 的图像如图所示,当
的图像如图所示,当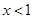 时,y的取值范围是 ( )
时,y的取值范围是 ( )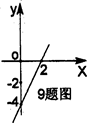
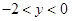
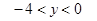
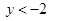
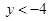
 的值为
的值为 
 和
和 的图像交于点
的图像交于点 ,根据图像可得方程
,根据图像可得方程 的解是
的解是 
 ,都有
,都有 .例如
.例如 ,那么
,那么 ,当
,当
 则
则 =
=  则
则 =" "
=" " ,其中
,其中
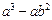 ; (2)
; (2)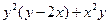 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号