江苏省姜堰市初一第一学期期末考试数学卷
如图7,在边长为a的正方形纸片的四个角都剪去一个长为m、宽为n的矩形.
(1)用含a,m,n的式子表示纸片剩余部分的面积;
(2)当m=3,n=5,且剩余部分的面积等于229时,求正方形的边长a的值
如图8,在△ABC中,D,E在直线BC上.
(1)若AB=BC=AC=CE=BD,求∠EAC的度数;
(2)若AB=AC=CE=BD,∠DAE=100°,求∠EAC的度数.
甲、乙两班参加植树活 动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为
动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为 (棵),乙班植树的总量为
(棵),乙班植树的总量为 (棵),两班一起植树所用的时间(从甲班开始植树时计时)为
(棵),两班一起植树所用的时间(从甲班开始植树时计时)为 (时),
(时), 、
、 分别与
分别与 之间的部分函数图象如图9
之间的部分函数图象如图9 所示.
所示.
(1)当0≤x≤6时,分别求 、
、 与
与 之间的函数关系式;
之间的函数关系式;
(2)如果甲、乙两班均保持前6个小时的工作效率,通过计算说明,当 时,甲、乙两班植树的总量之和能否超过
时,甲、乙两班植树的总量之和能否超过 棵.
棵.
如图10,C是线段AB上的一点,△ACD 和△BCE都是等边三角形.
和△BCE都是等边三角形.
 (1)求证:AE=BD;
(1)求证:AE=BD;
(2)若AE交CD于M,BD交CE于N,连结MN,试判断△MCN的形状,并说明理由.
方程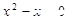 的根是 ( )
的根是 ( )
| A.x=0 | B.x=1 | C.x1=0,x2=1 | D.x1=0, x2= -1 |
下列事件中,属于必然性事件的是 ( )
| A.通常温度降到0℃以下,纯净的水结冰; |
| B.随意翻到一本书的某面,这页的页码是奇数; |
| C.购买一张彩票,中奖; |
| D.汽车累积行驶1万千米,从未出现故障. |
如图1,正方形的边长为a,以各边为直径在正方形内画半圆,图中阴影部分的面积是( )
A. |
B. |
C. |
D. |
袋子中有2个红球,3个绿球和4个蓝球,它们只有颜色上的区别,从袋子中随机地抽取一个球是绿球的概率是
如图2, 的顶点坐标分别为
的顶点坐标分别为
 .
.
(1) 画出将 绕
绕 点顺时针旋转
点顺时针旋转 的图形△A′B′C;
的图形△A′B′C;
(2) 点A′ 的坐标为 ;
(3) 求B点转过的路径长.
如图3,甲转盘被分成3个面积相等的扇形,乙转盘被分成2个面积相等的扇形.随机地转动指针(当指针指在边界线上时视为无效,重转).
请解答下列问题.
⑴ 在图甲中,随机地转动指针,指针指向扇形2的概率是_____________;
⑵ 分别转动图甲和图乙的指针,两个指针停止时所指区域内的数之和为6或7,试用树状图或列表法求出其概率.
如图4,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.
求BC、AD的长
如图5,做一个底面积为240cm2,长、宽、高的比为4∶2∶1的长方体,解答下列问题:
(1)这个长方体的长、宽、高分别是多少?
(2)长方体的表面积是多少?
(3)长方体的体积是多少?
已知x1,x2是关于x的一元二次方程x2-6x+k=0的两个实数根,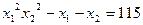 .
. (1) 求k的值;
(1) 求k的值;
2)求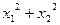 的值
的值
如图6,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于D、E,交AB于点C.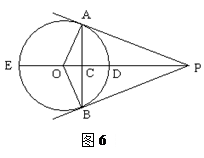
(1)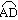 与
与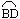 是否相等?说明理由;
是否相等?说明理由;
(2)OP与AB有怎样的位置关系?为什么?
如图7,利用一面墙(墙的最大可用长度为10米),用长为24米的篱笆围成中间隔有一道篱笆的长方形花圃ABCD.如果要在两个矩形的BC一边各开一个1.5米宽的门(做门材料不占用篱笆 ),且花圃的总面积为54
),且花圃的总面积为54 平方米,那么花圃的宽AB应为多少米?
平方米,那么花圃的宽AB应为多少米?
如图8,在Rt△ABC中,∠ACB=90°, ∠B=60°,BC=2.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α. 
解答下列问题:
(1) ① 当α=________度时,四边形EDBC是直角梯形;
② 当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;
(2) 当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
下列各组单项式中,是同类项的是 ( )
| A.-a2与(-a) 2 | B.2a2b与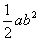 |
C.xyz与2xy | D.3x2y与3x2z |
下列说法中,正确的是( )
| A.倒数等于它本身的数是1 |
| B.如果两条线段不相交,那么它们一定互相平行 |
| C.等角的余角相等 |
| D.任何有理数的平方都是正数 |
如图,点O在直线AB上且OC⊥OD,若∠COA=36°则∠DOB的大小为( ) 
| A.36° | B.54° | C.64° | D.72° |
用一根长80 的绳子围成一个长方形,且长方形的长比宽长10
的绳子围成一个长方形,且长方形的长比宽长10 ,则这个长方形的面积是( )
,则这个长方形的面积是( )
A.25 |
B.45 |
C.375 |
D.1575 |
下表,填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
| A.38 | B.52 | C.66 | D.74 |
“激情盛会,和谐亚洲”第16届亚运会在中国广州举行,广州亚运城的建筑面积约是358000平方米,将358000用科学记数法表示为____________
如图所示,AB=4 cm.
(1)画图,延长AB到C,使BC=3 cm.
(2)如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?
如图,正方形网格的边长为1点P是 的边OB上的一点。
的边OB上的一点。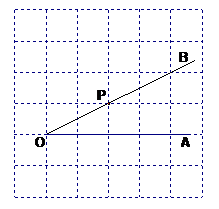
过点P画OB的垂线,交OA于点C;
过点P画OA的垂线,垂足为H;
点P到OA的距离为__________,因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为 和
和 ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
有一列数,第一个数为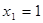 ,第二个数为
,第二个数为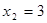 ,从第三个数开始依次为
,从第三个数开始依次为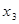 ,
,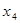 ,…
,…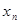 ,从第二个数开始,每个数是左右相邻两个数和的一半,如:
,从第二个数开始,每个数是左右相邻两个数和的一半,如: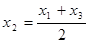 .
.
(1)求第三、第四、第五个数,并写出计算过程;
(2)根据(1)的结果,推测 =_______________;
=_______________;
(3)探索这一列数的规律,猜想第k个数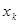 =_______________
=_______________
如图,将正方形纸片的两角分别折叠,使顶点A落在A′处,顶点D落在D′处,BC、BE为折痕,点B、A′、D′在同一条直线上。
(1)猜想折痕BC和BE的位置关系,并说明理由;
(2)写出图中∠D′BE的余角与补角;
(3)延长D′B、CA相交于点F,若∠EBD=330,求∠ABF和∠CBA的度数。
 ,其中
,其中

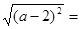 2-a,则a的取值范围是 ( )
2-a,则a的取值范围是 ( ) =
=  )是关于原点O的对称点,则
)是关于原点O的对称点,则 的值是
的值是 -
-
 取什么值时,关于
取什么值时,关于 的方程
的方程 有两个相等的实数根?并求出这时方程的根
有两个相等的实数根?并求出这时方程的根 =-9
=-9 =-9
=-9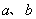 互为相反数,那么 ( )
互为相反数,那么 ( )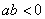
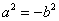
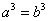
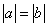


 、
、 在数轴上的位置如图所示,则
在数轴上的位置如图所示,则 的值
的值





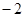 为解的一元一次方程为
为解的一元一次方程为 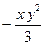 的系数是___
的系数是___ 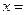 时,代数式
时,代数式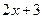 与
与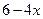 的值相等
的值相等
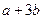 的值为
的值为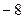 ,则代数式
,则代数式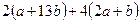 的值为_________
的值为_________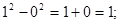

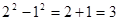 ;
; 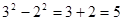 ;
;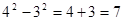 ;
; 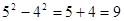 ; ……
; ……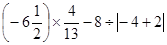
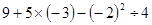

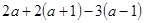
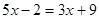
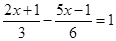
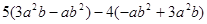 ,其中
,其中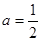 ,
,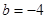
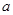 ,请用含
,请用含 粤公网安备 44130202000953号
粤公网安备 44130202000953号