北京市顺义区初三一模数学试题
已知:如图,在矩形 中,点
中,点 在对角线
在对角线 上,以
上,以 的长为半径的⊙
的长为半径的⊙ 与
与 ,
, 分别交于点E、点F,且∠
分别交于点E、点F,且∠ =∠
=∠ .
.
(1)判断直线 与⊙
与⊙ 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若 ,
, ,求⊙
,求⊙ 的半径.
的半径.
远洋电器城中,某品牌电视有 四种不同型号供顾客选择,它们每台的价格(单位:元)依次分别是:2500,4000,6000,10000.为做好下阶段的销售工作,商场调查了一周内这四种不同型号电视的销售情况,并根据销售情况,将所得的数据制成统计图,现已知该品牌一周内四种型号电视共售出240台,每台的销售利润占其价格的百分比如下表:
四种不同型号供顾客选择,它们每台的价格(单位:元)依次分别是:2500,4000,6000,10000.为做好下阶段的销售工作,商场调查了一周内这四种不同型号电视的销售情况,并根据销售情况,将所得的数据制成统计图,现已知该品牌一周内四种型号电视共售出240台,每台的销售利润占其价格的百分比如下表:
| 型号 |
A |
B |
C |
D |
| 利润 |
10% |
12% |
15% |
20% |

请根据以上信息,解答下列问题:
(1)请补全统计图;
(2)通过计算,说明商场这一周内该品牌哪种型号的电视总销售利润最大;
(3)谈谈你的建议.
在边长为1的正方形网格中,正方形 与正方形
与正方形 的位置如图所示.
的位置如图所示.
(1)请你按下列要求画图:
① 联结 交
交 于点
于点 ;
;
② 在 上取一点
上取一点 ,联结
,联结 ,
, ,使△
,使△ 与△
与△ 相似;
相似;
(2)若 是线段
是线段 上一点,连结
上一点,连结 并延长交四边形
并延长交四边形 的一边于点
的一边于点 ,且满足
,且满足 ,则
,则 的值为_____________.
的值为_____________.
已知抛物线 :
: 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求 的值;
的值;
(2) 时,抛物线
时,抛物线 向下平移
向下平移 个单位后与抛物线
个单位后与抛物线 :
: 关于
关于 轴对称,且
轴对称,且 过点
过点 ,求
,求 的函数关系式;
的函数关系式;
(3) 时,抛物线
时,抛物线 的顶点为
的顶点为 ,且过点
,且过点 .问在直线
.问在直线 上是否存在一点
上是否存在一点 使得△
使得△ 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点 的坐标, 如果不存在,请说明理由.
的坐标, 如果不存在,请说明理由.
已知:如图,正方形 中,
中, 为对角线,将
为对角线,将 绕顶点
绕顶点 逆时针旋转
逆时针旋转 °(
°( ),旋转后角的两边分别交
),旋转后角的两边分别交 于点
于点 、点
、点 ,交
,交 于点
于点 、点
、点 ,联结
,联结 .
.
(1)在 的旋转过程中,
的旋转过程中, 的大小是否改变,若不变写出它的度数,若改变,写出它的变化范围(直接在答题卡上写出结果,不必证明);
的大小是否改变,若不变写出它的度数,若改变,写出它的变化范围(直接在答题卡上写出结果,不必证明);
(2)探究△ 与△
与△ 的面积的数量关系,写出结论并加以证明.
的面积的数量关系,写出结论并加以证明.
已知二次函数 的图象与
的图象与 轴交于点
轴交于点 (
( ,0)、点
,0)、点 ,与
,与 轴交于点
轴交于点 .
.
(1)求点 坐标;
坐标;
(2)点 从点
从点 出发以每秒1个单位的速度沿线段
出发以每秒1个单位的速度沿线段 向
向 点运动,到达点
点运动,到达点 后停止运动,过点
后停止运动,过点 作
作 交
交 于点
于点 ,将四边形
,将四边形 沿
沿 翻 折,得到四边形
翻 折,得到四边形 ,设点
,设点 的运动时间为
的运动时间为 .
.
①当 为何值时,点
为何值时,点 恰好落在二次函数
恰好落在二次函数 图象的对称轴上;
图象的对称轴上;
②设四边形 落在第一象限内的图形面积为
落在第一象限内的图形面积为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的最大值.
的最大值.
据报道,北京市今年开工及建设启动的8条轨道交通线路,总投资约82 000 000 000元.
将82 000 000 000 用科学计数法表示为
A. |
B. |
C. |
D. |
一个布袋中有1个红球,3个黄球,4个蓝球,它们除颜色外完全相同. 从袋中随机取出一个球,取到黄球的概率是
A. |
B.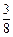 |
C.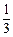 |
D.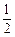 |
如图,中,AB=10,BC=6,E、F分别是AD、DC的中点,若EF=7,则四边形EACF的周长是
A.20 B.22 C.29 D.31
有20名同学参加“英语拼词”比赛,他们的成绩各不相同,按成绩取前10名参加复赛. 若小新知道了自己的成绩,则由其他19名同学的成绩得到的下列统计量中,可判断小新能否进入复赛的是
| A.平均数 | B.极差 | C.中位数 | D.方差 |
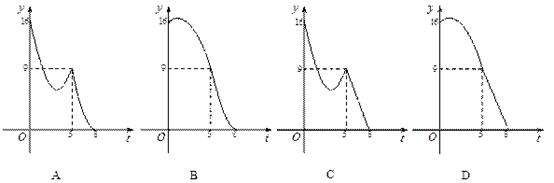
如图,在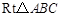 中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A
中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A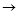 B
B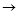 C的方向运动,到达点C时停止.设
C的方向运动,到达点C时停止.设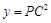 ,运动时间为t秒,则能反映y与t之间函数关系的大致图象是
,运动时间为t秒,则能反映y与t之间函数关系的大致图象是 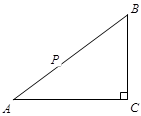
如图,矩形纸片 中,
中, .第一次将纸片折叠,使点
.第一次将纸片折叠,使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 ,第二次将纸片折叠使点
,第二次将纸片折叠使点 与点
与点 重合,折痕与
重合,折痕与 交
交 于点
于点 ;设
;设 的中点为
的中点为 ,第三次将纸片折叠使点
,第三次将纸片折叠使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ,… .按上述方法折叠,第n次折叠后的折痕与
,… .按上述方法折叠,第n次折叠后的折痕与 交于点
交于点 ,则
,则 =" " ,
=" " , =" " .
=" " .

如图,点C、D 在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD, CO=DO, .求证:AE=BF.
.求证:AE=BF.
如图,一次函数 与反比例函数
与反比例函数 的图象交于A(2,1),B(-1,
的图象交于A(2,1),B(-1, )两点.
)两点.
(1)求k和b的值;
(2)结合图象直接写出不等式 的解集.
的解集.
.列方程或方程组解应用题:
“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件?
| 积分兑换礼品表 |
|
| 兑换礼品 |
积分 |
| 电茶壶一个 |
7000分 |
| 保温杯一个 |
2000分 |
| 牙膏一支 |
500分 |
某区在一次扶贫助残活动中,共捐款136 000元.将136 000元用科学记数法表示为
A. 元 元 |
B. 元 元 |
C. 元 元 |
D. 元 元 |
某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数分别为6 , 10 , 5 , 3 , 4 , 8 , 4 ,这组数据的中位数和极差分别是
| A.4, 7 | B.5, 7 | C.7, 5 | D.3, 7 |
如图,A、B是函数 的图象上关于原点对称的任意两点,BC∥
的图象上关于原点对称的任意两点,BC∥ 轴,AC∥
轴,AC∥ 轴,△ABC的面积记为
轴,△ABC的面积记为 ,则
,则
A.  B.
B.  C.
C.  D.
D.
将除去零以外的自然数按以下规律排列,根据第一列的奇数行的数的规律,写出第一列第9行的数为 ,再结合第一行的偶数列的数的规律,判断2011所在的位置是第 行第 列.
列方程或方程组解应用题:
我区教委要求各学校师生开展“彩虹读书活动”. 某校九年级一班和九年级二班的学生向学校图书馆借课外读物共196本,一班为每位学生借3本,二班 为每位学生借2本,一班借的课外读物数量比二班借的课外读物数量多44本,求九年级一班和二班各有学生多少人?
为每位学生借2本,一班借的课外读物数量比二班借的课外读物数量多44本,求九年级一班和二班各有学生多少人?
.已知:如图,梯形ABCD中,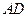 ∥
∥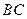 ,
,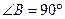 ,
,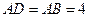 ,
,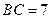 ,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点
,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点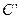 处.
处.
(1)求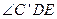 的度数;
的度数;
(2)求△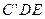 的面积.
的面积.
学校为了学生的身体健康,每天开展体育活动一小时,开设排球、篮球、羽毛球、体操课.学生可根据自己的爱好任选其中一项,老师根据学生报名情况进行了统计,并绘制 了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题: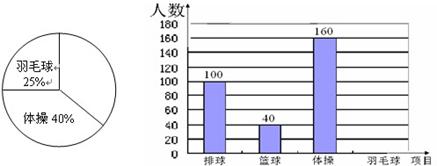
(1)该校学生报名总人数有多少人?
(2)从表中可知选羽毛球的学生有多少人?选排球和篮球的人数分别占报名总人数的百分之几?
(3)将两个统计图补充完整.
如图,将正方形沿图中虚线(其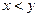 )剪成① ② ③ ④ 四块图形,用这四块图形恰好能拼成一个矩形(非正方形).
)剪成① ② ③ ④ 四块图形,用这四块图形恰好能拼成一个矩形(非正方形).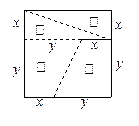
(1)画出拼成的矩形的简图;
(2)求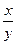 的值.
的值.
已知:关于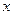 的一元二次方程
的一元二次方程
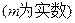
(1) 若方程有两个不相等的实数根,求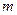 的取值范围;
的取值范围;
(2)求证:无论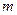 为何值,方程总有一个固定的根;
为何值,方程总有一个固定的根;
(3)若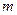 为整数,且方程的两个根均为正整数,求
为整数,且方程的两个根均为正整数,求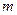 的值.
的值.
已知:如图,等边△ABC中,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.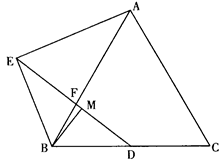
(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7 ,AE=
,AE= ,
,
求tan∠BCP的值.



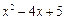 变形,所得结果是
变形,所得结果是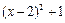
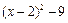
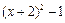
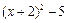
 有意义,则x的取值范围是 .
有意义,则x的取值范围是 . = .
= .
 .
.
 是方程
是方程 的一个实数根,求代数式
的一个实数根,求代数式 的值.
的值.
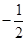 的绝对值是
的绝对值是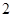
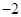



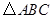 内接于圆
内接于圆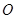 ,
, ,
,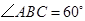 ,
,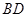 是圆
是圆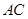 于点
于点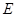 ,连结
,连结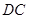 ,则
,则 等于
等于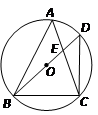
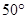
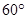
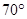
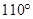
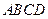 中,
中,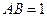 ,
,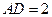 ,
, 是
是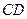 的中点,点
的中点,点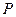 在矩形的边上沿
在矩形的边上沿
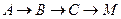 运动,则
运动,则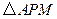 的面积
的面积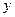 与点
与点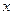 之间的函数关系用图象表示大致是下图中的
之间的函数关系用图象表示大致是下图中的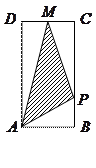
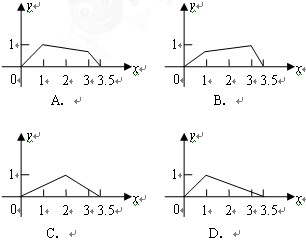
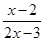 有意义,则
有意义,则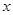 的取值范围是 .
的取值范围是 .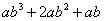 = .
= .
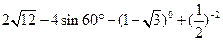

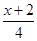 ≤
≤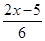 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来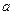 是一元二次方程
是一元二次方程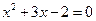 的实数根,求代数式
的实数根,求代数式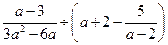 的值.
的值. 中,
中, ,
, 于
于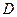 ,
,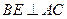 于
于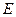 ,
,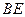 与
与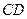 相交于点
相交于点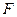 .求证:
.求证: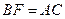 ;
;
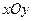 中,一次函数
中,一次函数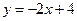 的图象分别与
的图象分别与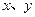 轴交于点A、 B,点
轴交于点A、 B,点 在
在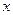 轴上,若
轴上,若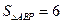 ,求直线PB的函数解析式.
,求直线PB的函数解析式.
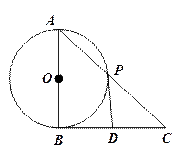
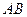 是
是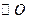 的直径,
的直径,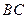 切
切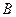 ,
,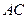 交
交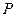 ,
, 为
为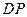 .
.
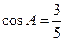 ,
, 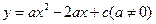 与
与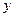 轴交于点
轴交于点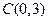 ,与
,与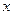 轴交于
轴交于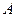 、
、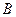 两点,点
两点,点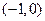 .
.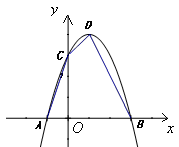
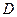 的坐标;
的坐标;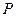 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形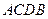 面积相等的四边形
面积相等的四边形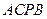 的点
的点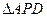 的面积.
的面积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号