已知二次函数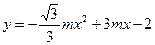 的图象与
的图象与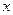 轴交于点
轴交于点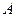 (
(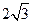 ,0)、点
,0)、点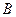 ,与
,与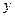 轴交于点
轴交于点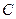 .
.
(1)求点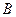 坐标;
坐标;
(2)点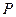 从点
从点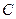 出发以每秒1个单位的速度沿线段
出发以每秒1个单位的速度沿线段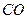 向
向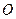 点运动,到达点
点运动,到达点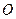 后停止运动,过点
后停止运动,过点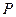 作
作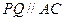 交
交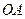 于点
于点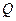 ,将四边形
,将四边形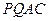 沿
沿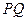 翻 折,得到四边形
翻 折,得到四边形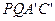 ,设点
,设点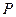 的运动时间为
的运动时间为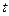 .
.
①当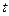 为何值时,点
为何值时,点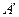 恰好落在二次函数
恰好落在二次函数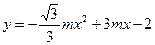 图象的对称轴上;
图象的对称轴上;
②设四边形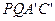 落在第一象限内的图形面积为
落在第一象限内的图形面积为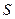 ,求
,求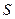 关于
关于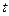 的函数关系式,并求出
的函数关系式,并求出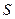 的最大值.
的最大值.
相关知识点
推荐套卷
已知二次函数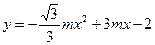 的图象与
的图象与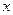 轴交于点
轴交于点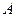 (
(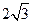 ,0)、点
,0)、点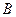 ,与
,与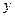 轴交于点
轴交于点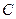 .
.
(1)求点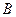 坐标;
坐标;
(2)点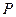 从点
从点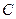 出发以每秒1个单位的速度沿线段
出发以每秒1个单位的速度沿线段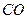 向
向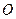 点运动,到达点
点运动,到达点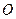 后停止运动,过点
后停止运动,过点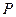 作
作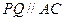 交
交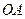 于点
于点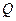 ,将四边形
,将四边形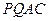 沿
沿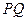 翻 折,得到四边形
翻 折,得到四边形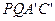 ,设点
,设点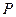 的运动时间为
的运动时间为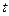 .
.
①当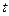 为何值时,点
为何值时,点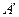 恰好落在二次函数
恰好落在二次函数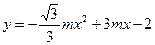 图象的对称轴上;
图象的对称轴上;
②设四边形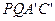 落在第一象限内的图形面积为
落在第一象限内的图形面积为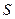 ,求
,求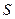 关于
关于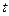 的函数关系式,并求出
的函数关系式,并求出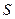 的最大值.
的最大值.