北京市海淀区初三一模数学试题
抛物线 的部分图象如图所示,请写出与其关系式、图象相关的2个正确结论: , .(对称轴方程,图象与x正半轴、y轴交点坐标例外)
的部分图象如图所示,请写出与其关系式、图象相关的2个正确结论: , .(对称轴方程,图象与x正半轴、y轴交点坐标例外)
把抛物线y=ax +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x -3x+5
-3x+5 ,则a+b+c=__________
,则a+b+c=__________
二次函数 的图象如图所示,点
的图象如图所示,点 位于坐标原点, 点
位于坐标原点, 点 ,
, ,
, ,…,
,…, 在y轴的正半轴上,点
在y轴的正半轴上,点 ,
, ,
, ,…,
,…,  在二次函数
在二次函数
位于第一象限的图象上, 若△ ,△
,△ ,△
,△ ,…,△
,…,△
都为等边三角形,则△ 的边长=
的边长= 
已知二次函数y=- x2 –x+4回答下列问题
x2 –x+4回答下列问题
(1)用配方法将其化成y="a" (x-h)2+k的形式
(2)指出抛物线的顶点坐标和对称轴
(3)当x取何值时,y随x增大而增大;
当x取何值时,y随x增大而减小?
已知二次函 的图象过点(0, 5)
的图象过点(0, 5)
⑴ 求m的值,并写出二次函数的关系式;
⑵ 求出二次函数图象的顶点坐标、对称轴.
已知如图,二次函数y="ax2" +b x+c的图像过A、B、C三点
x+c的图像过A、B、C三点
观察图像写出A、B、C三点的坐标
求出二次函数的解析式
已知:o为坐标原点,∠ AOB=300 , ∠ABO=900 且A(2,0)求: 过A、B、O三点的二次函数解析式
已知二次函数 中,函数
中,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表:
 |
… |
 |
 |
 |
 |
 |
 |
… |
 |
… |
 |
 |
 |
 |
 |
 |
… |
(1)求该二次函数的关系式;( 2)当
2)当 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若 ,
, 两点都在该函数的图象上,试比较
两点都在该函数的图象上,试比较 与
与 的大小.
的大小.
用配方法将二次三项式a2+4a+5变形,结果为( )
| A.(a-2)2+1 | B.(a+2)2+1 | C.(a-2)2-1 | D.(a+2)2-1 |
下列命题为假命题的是( )
| A.有一个外角的平分线平行于一边的三角形是等腰三角形 |
| B.到三角形三边距离相等的点是三角形角平分线的交点 |
| C.斜边和一条直角对应相等的两个直角三角形全等 |
| D.平行线间的线段相等 |
三角形两边长分别为3和6,第三边是方程x2-6x+8=0的解,则 这个三角形的周长是( )
这个三角形的周长是( )
| A.11 | B.13 | C.11或13 | D.无法确定 |
在△ABC中,∠B,∠C的平分线相交于点F,过F作DE∥BC,交AB于D,交AC于E,则 (1)△BDF,△CEF都是等腰三角形 (2)DE=BD+CE (3)AD+DE+AE=AB+AC (4)BF=CF 其中正确的是( )
| A.仅(2) | B.仅(1)(2) | C.除(4)外正确 | D.全部正确 |
如果菱形的周长为高度的8倍,则菱形较小的内角的度数为( )
| A.150° | B.60° | C.45° | D.30° |
在宽为40m,长为64m的矩形广场上,修建同样宽的三条道路,两条纵向,一条横向,并且互相垂直,把耕地分成面积相等的六块作为草坪,要使草坪面积为2418m2,若道路宽为xm,根据题意列出方程为 ( )
| A.(64-2x)(40-x)=2418 | B.(64-x)(40-2x) =2418 |
| C.40x+64x-2x2=2418 | D.(64-x)(40-x)=2418 |
如图,在直角梯形ABCD中,∠B=90°,DC∥AB,动点P从B点出发,沿折线B→C→D→A运动,设点P运动的路程为x,△ABP的面积为y,如果关于x的函数y的图像如图2所示,则△ABC的面积为( )
| A.10 | B.16 | C.18 | D.32 |
若一元二次方程(m-2)x2+3(m2+15)x+m2-4=0的常数项为0,则m的值为___.
如图,AB=AD,∠1=∠2,添加一个适当的条件,使△ABC≌ADE,则添加的条件是____.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为 .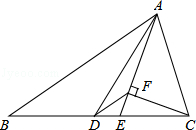
据报道,北京市今年开工及建设启动的8条轨道交通线路,总投资约82 000 000 000元.
将82 000 000 000 用科学计数法表示为
A. |
B. |
C. |
D. |
一个布袋中有1个红球,3个黄球,4个蓝球,它们除颜色外完全相同. 从袋中随机取出一个球,取到黄球的概率是
A. |
B.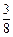 |
C.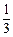 |
D.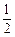 |
如图,中,AB=10,BC=6,E、F分别是AD、DC的中点,若EF=7,则四边形EACF的周长是
A.20 B.22 C.29 D.31
有20名同学参加“英语拼词”比赛,他们的成绩各不相同,按成绩取前10名参加复赛. 若小新知道了自己的成绩,则由其他19名同学的成绩得到的下列统计量中,可判断小新能否进入复赛的是
| A.平均数 | B.极差 | C.中位数 | D.方差 |
如图,在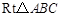 中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A
中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A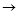 B
B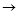 C的方向运动,到达点C时停止.设
C的方向运动,到达点C时停止.设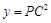 ,运动时间为t秒,则能反映y与t之间函数关系的大致图象是
,运动时间为t秒,则能反映y与t之间函数关系的大致图象是 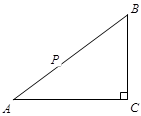
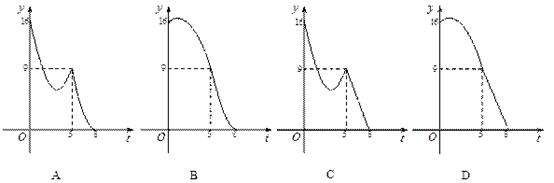
如图,矩形纸片 中,
中, .第一次将纸片折叠,使点
.第一次将纸片折叠,使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 ,第二次将纸片折叠使点
,第二次将纸片折叠使点 与点
与点 重合,折痕与
重合,折痕与 交
交 于点
于点 ;设
;设 的中点为
的中点为 ,第三次将纸片折叠使点
,第三次将纸片折叠使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ,… .按上述方法折叠,第n次折叠后的折痕与
,… .按上述方法折叠,第n次折叠后的折痕与 交于点
交于点 ,则
,则 =" " ,
=" " , =" " .
=" " .

如图,点C、D 在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD, CO=DO, .求证:AE=BF.
.求证:AE=BF.
如图,一次函数 与反比例函数
与反比例函数 的图象交于A(2,1),B(-1,
的图象交于A(2,1),B(-1, )两点.
)两点.
(1)求k和b的值;
(2)结合图象直接写出不等式 的解集.
的解集.
.列方程或方程组解应用题:
“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件?
| 积分兑换礼品表 |
|
| 兑换礼品 |
积分 |
| 电茶壶一个 |
7000分 |
| 保温杯一个 |
2000分 |
| 牙膏一支 |
500分 |
如图,AB 为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
(1)证明BF是⊙O的切线;
(2)设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.
为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示). 
(1)请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率 ;
;
(3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?
如图1,已知等边△ABC的边长为1,D、E、F分别是AB、BC、AC边上的点(均不与点A、B、C重合),记△DEF的周长为 .
.
(1)若D、E、F分别是AB、BC、AC边上的中点,则 =_______;
=_______;
(2)若D、E、F分别是AB、BC、AC边上任意点,则 的取值范围是 .
的取值范围是 .
小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将 以AC边为轴翻折一次得
以AC边为轴翻折一次得 ,再将
,再将 以
以 为轴翻折一次得
为轴翻折一次得 ,如图2所示. 则由轴对称的性质可知,
,如图2所示. 则由轴对称的性质可知, ,根据两点之间线段最短,可得
,根据两点之间线段最短,可得 . 老师听了后说:“你的想法很好,但
. 老师听了后说:“你的想法很好,但 的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.
的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.
已知关于 的方程
的方程 .
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于4且小于8,求m的取值范围;
(3)设抛物线 与
与 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求 的值.
的值.
.已知平面直角坐标系xOy中, 抛物线 与直线
与直线 的一个公共点为
的一个公共点为 .
.
(1)求此抛物线和直线的解析式;
(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ长度的最大值;
(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.
 与
与 的两交点关于原点对称,则
的两交点关于原点对称,则 分别为 .
分别为 . 解为____.
解为____.


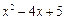 变形,所得结果是
变形,所得结果是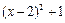
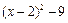
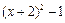
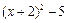
 有意义,则x的取值范围是 .
有意义,则x的取值范围是 . = .
= .
 .
.
 是方程
是方程 的一个实数根,求代数式
的一个实数根,求代数式 的值.
的值.
 . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
 ,则k =" " ;
,则k =" " ; 粤公网安备 44130202000953号
粤公网安备 44130202000953号