．已知平面直角坐标系xOy中, 抛物线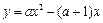
与直线
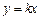的一个公共点为
.
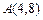（1）求此抛物线和直线的解析式；
（2）若点P在线段OA上，过点P作y轴的平行线交（1）中抛物线于点Q，求线段PQ长度的最大值；
（3）记（1）中抛物线的顶点为M，点N在此抛物线上，若四边形AOMN恰好是梯形，求点N的坐标及梯形AOMN的面积.
,其中
）·（
），其中
其中x＝
，其中
.
，其中
.相关知识点
推荐套卷
．已知平面直角坐标系xOy中, 抛物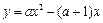线与直线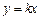的一个公共点为.
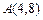（1）求此抛物线和直线的解析式；
（2）若点P在线段OA上，过点P作y轴的平行线交（1）中抛物线于点Q，求线段PQ长度的最大值；
（3）记（1）中抛物线的顶点为M，点N在此抛物线上，若四边形AOMN恰好是梯形，求点N的坐标及梯形AOMN的面积.
粤公网安备 44130202000953号