河南省周口市初三下学期第二十八章锐角三角函数检测题
如图,中,AB=10,BC=6,E、F分别是AD、DC的中点,若EF=7,则四边形EACF的周长是
A.20 B.22 C.29 D.31
有20名同学参加“英语拼词”比赛,他们的成绩各不相同,按成绩取前10名参加复赛. 若小新知道了自己的成绩,则由其他19名同学的成绩得到的下列统计量中,可判断小新能否进入复赛的是
| A.平均数 | B.极差 | C.中位数 | D.方差 |
如图,在 中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A
中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A B
B C的方向运动,到达点C时停止.设
C的方向运动,到达点C时停止.设 ,运动时间为t秒,则能反映y与t之间函数关系的大致图象是
,运动时间为t秒,则能反映y与t之间函数关系的大致图象是 

如图,矩形纸片 中,
中, .第一次将纸片折叠,使点
.第一次将纸片折叠,使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 ,第二次将纸片折叠使点
,第二次将纸片折叠使点 与点
与点 重合,折痕与
重合,折痕与 交
交 于点
于点 ;设
;设 的中点为
的中点为 ,第三次将纸片折叠使点
,第三次将纸片折叠使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ,… .按上述方法折叠,第n次折叠后的折痕与
,… .按上述方法折叠,第n次折叠后的折痕与 交于点
交于点 ,则
,则 =" " ,
=" " , =" " .
=" " .

如图,点C、D 在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD, CO=DO,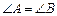 .求证:AE=BF.
.求证:AE=BF.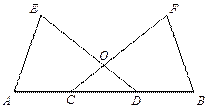
如图,一次函数 与反比例函数
与反比例函数 的图象交于A(2,1),B(-1,
的图象交于A(2,1),B(-1,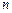 )两点.
)两点.
(1)求k和b的值;
(2)结合图象直接写出不等式 的解集.
的解集.
.列方程或方程组解应用题:
“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件?
| 积分兑换礼品表 |
|
| 兑换礼品 |
积分 |
| 电茶壶一个 |
7000分 |
| 保温杯一个 |
2000分 |
| 牙膏一支 |
500分 |
如图,AB 为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
为⊙O的直径,AB=4,点C在⊙O上, CF⊥OC,且CF=BF.
(1)证明BF是⊙O的切线;
(2)设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.
为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示). 
(1)请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率 ;
;
(3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?
某区在一次扶贫助残活动中,共捐款136 000元.将136 000元用科学记数法表示为
A. 元 元 |
B. 元 元 |
C. 元 元 |
D. 元 元 |
某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数分别为6 , 10 , 5 , 3 , 4 , 8 , 4 ,这组数据的中位数和极差分别是
| A.4, 7 | B.5, 7 | C.7, 5 | D.3, 7 |
如图,A、B是函数 的图象上关于原点对称的任意两点,BC∥
的图象上关于原点对称的任意两点,BC∥ 轴,AC∥
轴,AC∥ 轴,△ABC的面积记为
轴,△ABC的面积记为 ,则
,则
A.  B.
B.  C.
C.  D.
D.
如图:P是∠ 的边OA上一点,且P点的坐标为(3,4),则sin
的边OA上一点,且P点的坐标为(3,4),则sin =_____________.
=_____________.
.如图,△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD= , tan∠BCE=
, tan∠BCE= ,那么CE=
,那么CE= 
如图:在直角三角形ABC中,∠ACB=90º,∠A﹤∠B,以AB边上的中线CM为折痕将ACM折叠,使点A落在点D处,如果CD恰好与AB垂直,则tan A=___
在中,如果各边的长度同时扩大2倍,那么锐角A的正弦值和余弦值______
| A.都扩大2倍 | B.都缩小2倍 | C.都不变 | D.不能确定 |
.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3, AB=8,则tan∠OPA的值为( )
| A.3 | B.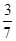 |
C.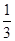 或 或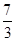 |
D.3或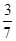 |
如图:在等腰△ABC中,∠C=90º,AC=6,D 是AC上一点,若tan∠DBA=,则A D的长为( )

A. |
B.2 | C.1 | D.2 |
如图:某市在“旧城改造”中计划在市内一块三角形空地上种植某种草皮来美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( )元。
| A.450a | B.225a | C.150a | D.300a |
如图:在平行四边形ABCD中, AB:AD =3:2, ∠ADB=60º,那么 A的值等于
A的值等于

A. |
B. |
C. |
D. |
已知AB和CD分别是半圆O的直径和弦,AD和BC的夹角为a,则S△CDE: S△ABE等于( ) 
| A.Sin2a | B.cos2a | C.tan2a | D. sina |
小阳发现电线杆AB的影子落在土坡的破面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30º 角,且此时测得1米杆的影长为2米,则 电线杆的高度为( )

| A.9米 | B.28米 | C.(7+ )米 )米 |
D.(14+ 2 )米 )米 |
、如图:在平面直角坐标系中,直线AB与x轴的夹角为60º,且点A的坐标为(–2,0),点B在x轴的上方,设AB=a,那么点B的坐标为( )
、已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
.如图,已知:在△ABC中,∠A=60 ,∠B=45
,∠B=45 ,AB=8.求△ABC的面积(结果可保留根号)。
,AB=8.求△ABC的面积(结果可保留根号)。
 有意义,则x的取值范围是 .
有意义,则x的取值范围是 . = .
= .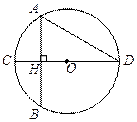
 .
.
 是方程
是方程 的一个实数根,求代数式
的一个实数根,求代数式 的值.
的值.
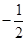 的绝对值是
的绝对值是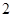
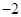



 )=
)= ,则∠A=" " .
,则∠A=" " . 。
。 则sin
则sin =__________,2tan2β=_________.
=__________,2tan2β=_________. A =
A = ,则tan B=( )
,则tan B=( )



 45
45 -
- +
+ +6 tan30
+6 tan30
 tan30°-tan45°
tan30°-tan45° ≈1.73
≈1.73 粤公网安备 44130202000953号
粤公网安备 44130202000953号