初中数学圆解答题

如图，在 $△ABC$中，点 $O$是 $AC$边上（端点除外）的一个动点，过点 $O$作直线 $MN//BC$．设 $MN$交 $\angle BCA$的平分线于点 $E$，交 $\angle BCA$的外角平分线于点 $F$，连接 $AE$、 $AF$．那么当点 $O$运动到何处时，四边形 $AECF$是矩形？并证明你的结论．

已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．

手工课上，小明准备做一个形状是菱形的风筝，这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位：cm²)随其中一条对角线的长x(单位：cm)的变化而变化．
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
(2)当x是多少时，菱形风筝面积S最大?最大面积是多少?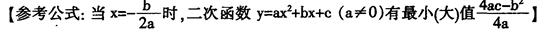

如图，四边形ABCD是平行四边形，AC是对角线，BE⊥AC，垂足为E，DF⊥AC ，垂足为F.求证DF=BE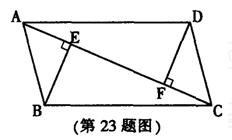

（本小题满分10分）在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，
对角线AC与BD相交于点O，线段OA，OB的中点分别为E，F。
（1）求证：△FOE≌△DOC；
（2）求sin∠OEF的值；
（3）若直线EF与线段AD，BC分别相交于点G，H，求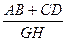的值。

11·西宁）（本小题满分8分）如图12 ，矩形ABCD的对角线相交于点O，DE∥CA，AE∥BD．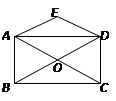

（1）求证：四边形AODE是菱形；
（2）．若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，
其余条件不变，则四边形AODE是_  ▲  ．

(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.

如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．
⑴说明四边形ACEF是平行四边形；
⑵当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．

（11·台州）(10分)丁丁想在一个矩形材料中剪出如图阴影所示的梯形，作为要制作的风筝的一个翅膀．请你根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位，≈1.7)．

（11·台州）(8分)如图，分别延长□ABCD的边BA、DC到点E、H，使得AE
＝AB，CH＝CD，连接EH，分别交AD、BC于点F、G．
求证：△AEF≌△CHG．

已知：如图9，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0, 6 )，D ( 4，6），且AB＝.

（1）求点B的坐标；
（2）求经过A、B、D三点的抛物线的解析式；
（3）在（2）中所求的抛物线上是否存在一点P，

图9

使得?若存在，请求出该点坐标，

若不存在，请说明理由.

如图，在矩形ABCD中，AD=4，AB=m(m＞4)，点P是AB边上的任意一点（不与A、B重合），连结PD，过点P作PQ⊥PD，交直线BC于点Q．
(1)当m=10时，是否存在点P使得点Q与点C重合？若存在，求出此时AP的长；若不存在，说明理由；
(2)连结AC，若PQ∥AC,求线段BQ的长（用含m的代数式表示）
(3)若△PQD为等腰三角形，求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式，并写出m的取值范围．

证明题24．如图8，在  ABCD中，DE＝BF.

求证：四边形AFCE是平行四边形.

 

（11·湖州）（本小题10分）
如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。
⑴求证：四边形AECF是平行四边形；
⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。

数学课上，李老师出示了这样一道题目：如图，正方形的边长为，为边延长线上的一点，为的中点，的垂直平分线交边于，交边的延长线于.当时，与的比值是多少？
经过思考，小明展示了一种正确的解题思路：过作直线平行于交，分别于，，如图，则可得：，因为，所以.可求出和的值，进而可求得与的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究，得出了的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.