(11·肇庆)(本小题满分7分)
如罔7,在一方形ABCD中.E为对角线AC上一点,连接EB、ED,
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
(8分)在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
(12分)如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点
A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速
度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后
第ts时,△E FG的面积为Scm2
FG的面积为Scm2 .
.
(1)当t=1s时,S的值是多少?
(2)写出S与t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似?请说明理由。
如图(图1、图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,FN⊥BC,交BC的延长线于点N。
(1)若点E是BC的中点(如图1),AE与EF相等吗?为什么?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值。
如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
(1)求证:∠ABD=∠CBD;
(2)若∠C=2∠E,求证:AB=DC;
(3)在(2)的条件下, 求四边形AEBD的面积.
求四边形AEBD的面积.
(本题满分9分) 如图8,等腰梯形ABCD中,AB∥CD,AD=BC.将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合.
(1)点C是否在以AB为直径的圆上?请说明理由;
(2)当AB=4时,求此梯形的面积.
.如图(1),在直角△ABC中, ∠ACB=90 ,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).
,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=nEA(m,n为实数).
试探究线段EF与EG的数量关系.
(1)如图(2),当m=1,n=1时,EF与EG的数量关系是
证明:
(2) 如图(3),当m=1,n为任意实数时,EF与EG的数量关系是
证明
(3)如图(1),当m,n均为任意实数时,EF与EG的数量关系是
(写出关系式,不必证明)
选做题:从 甲、乙两题中选做一题,如果两题都做,只以甲题计分。
甲、乙两题中选做一题,如果两题都做,只以甲题计分。
题甲:已知关于 的方程
的方程 的两根为
的两根为 、
、 ,且满足
,且满足 .求
.求 的值。
的值。
题乙:如图12,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
(1)求证:AC⊥BD
(2)求△AOB的面积
我选做的是 题
(11·钦州) 如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.
如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.
如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
如图,在平行四边形ABCD中,E为BC中点,AE的延长线与DC的延长线相交于点F.
(1)证明:∠DFA=∠FAB;
(2)证明:△ABE≌△FCE.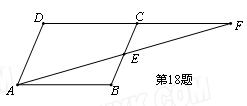
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD 上.
上.
(1)求证:△ABE∽△DFE
(2)若sin∠DFE=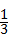 ,求tan∠EBC的值.
,求tan∠EBC的值.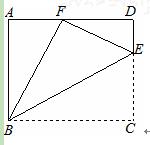
如图,等腰梯形ABCD中,AD∥BC,点E,F在BC上, 且BE=FC,连接DE,AF.求证:DE=AF.
且BE=FC,连接DE,AF.求证:DE=AF.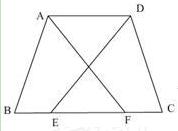
如 图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.