．如图，四边形ABCD的对角线AC、DB相交于点O，现给出如下三个条件：
.
（1）请你再增加一个条件：________，使得四边形ABCD为矩形（不添加其它字母和辅助线，只填一个即可，不必证明）；
（2）请你从
中选择两个条件________（用序号表示，只填一种情况），使得
，并加以证明.
四边形ABCD、DEFG都是正方形，连接AE、CG．
（1）求证：AE=CG；
（2）观察图形，猜想AE与CG之间的位置关系，并证明你的猜想．
如图7，菱形ABCD中，E是对角线AC上一点．
（1）求证：△ABE≌△ADE；
（2）若AB=AE，∠BAE=36º，求∠CDE的度数．
(本题满分8分)
如图，E、F分别是平行四边形ABCD对角线BD所在直线上两点，BE=DF，请你以F为一个端点，和图中己标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只需研究一组线段相等即可）
（1）连结_________
（2）猜想：_________
（3）证明：
（本小题满分10分）
如图（1
）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图（2）所示．
已知展开图中每个正方形的边长为1．
（1）求在该展开图中可画出最长线段的长度？这样的线段可画几条？
（2）试比较立体图中
与平面展开图中
的大小关系？
如图，在直角坐标系中，点A的坐标为（0，8），点 B（b，t）在直线x=b上运动，点D、E、F分别为OB、0A、AB的中点，其中b是大于零的常数．
（1）判断四边形DEFB的形状．并证明你的结论；
（2）试求四边形DEFB的面积S与b的关系式；
（3）设直线x=b与x轴交于点C，问：四边形DEFB能不能是矩形？若能．求出t的值；若不能，说明理由．
（本小题满分14分）如图，在等腰梯形ABCD中，AB=DC=5，AD=4，BC="10." 点
E在下底边BC上，点F在腰AB上. 
（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积；
（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；
（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分？若存在，求出此时BE的长；若不存在，请说明理由.
（本小题满分8分）如图，O是菱形ABCD对角线的交点，作DE∥AC，CE∥BD，DE、CE交于点E，四边形OCED是矩形吗？证明你的结论。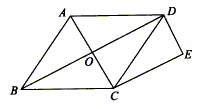
如图，在▱ABCD中，E，F分别是BC，AD中点．
（1）求证：△ABE≌△CDF；
（2）当BC=2AB=4，且△ABE的面积为
，求证：四边形AECF是菱形．
如图①，在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个 三角形
（2）如图②、在矩形ABCD中，AB=2，BC=4，，当它的“折痕△BEF”的顶点E位于AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；
（3）如图③，在矩形ABCD中，AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？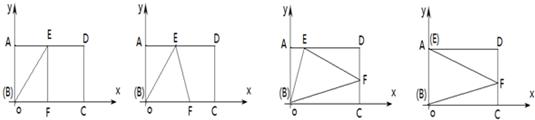
在正方形ABCD中，点G是BC上任意一点，连接AG，过B，D两点分别作BE⊥AG，DF⊥AG，垂足分别为E，F两点，求证：△ADF≌△BAE．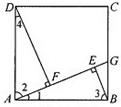
已知，E、F是四边形ABCD的对角线AC上的两点，AE=CF，BE=DF，BE∥DF．求证：四边形A BCD是平行四边形．
如图，已知四边形ABCD是平行四边形．
（1）求证：△MEF∽△MBA；
（2）若AF、BE分别是∠DAB，∠CBA的平分线，求证：DF=EC．
如图，在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ．
（1）求证：△BDQ≌△ADP；
（2）已知AD=3，AP=2，求cos∠BPQ的值（结果保留根号）．
粤公网安备 44130202000953号