浙江省衢州华茂八年级下学期第二次月考数学试卷
如图:抛物线 与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
⑴求抛物线的对称轴和点B的坐标;
⑵过点C作CP⊥对称轴于点P,连结BC交对称轴于点D,连结AC、BP,且  ,求
,求 抛物线的解析式;
抛物线的解析式;
⑶在⑵的条件下,设抛物线的顶点为G,连结BG、CG、求 BCG的面积。
BCG的面积。
据媒体报道,我国因环境问题造成的经济损失每年高达680 000 000元,这个数用科学记数法可表示为( ).
A.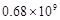 |
B.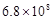 |
C.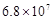 |
D. |
为了从甲、乙、丙三位同学中选派一位同学参加环保知识竞赛,老师对他们的五次环保知识测验成绩进行了统计,他们的平均分均为85分,方差分别为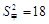 ,
,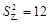 ,
,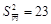 . 根据统计结果,应派去参加竞赛的同学是 .(填“甲、乙、丙”中的一个)
. 根据统计结果,应派去参加竞赛的同学是 .(填“甲、乙、丙”中的一个)
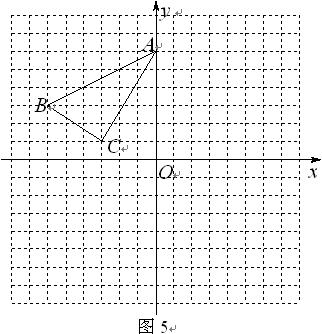
△ABC在方格纸中的位置如图5所示,方格纸中的每个小正方形的边长为1个单位.
(1)△ 与△ABC关于纵轴(
与△ABC关于纵轴( 轴)对称,请你在图5中画出△
轴)对称,请你在图5中画出△ ;
;
(2)将△ABC向下平移8个单位后得到△ ,请你在图5中画出△
,请你在图5中画出△ .
.
如图6,小明以3米/秒的速度从山脚A点爬到山顶B点,已知点B到山脚的垂直距离 为24米,且山坡坡角
为24米,且山坡坡角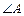 的度数为
的度数为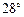 ,问小明从山脚爬上山顶需要多少时间?(结果精确到
,问小明从山脚爬上山顶需要多少时间?(结果精确到 )(参考数据:
)(参考数据: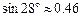 ,
,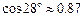 ,
,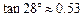 )
)
如图7, 是⊙
是⊙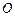 的直径,AC与⊙
的直径,AC与⊙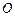 相切,切点为A,D为⊙
相切,切点为A,D为⊙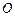 上一点,AD与OC相交于点E,且
上一点,AD与OC相交于点E,且 .
.
(1)求证: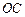 ∥
∥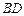 ;
;
(2)若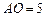 ,
,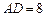 ,求线段CE的长.
,求线段CE的长.
在一个不透明的口袋中装有白、黄两种颜色的乒乓球(除颜色外其余都相同),其中黄球有1个,从袋中任意摸出一个球是黄球的概率为 .
.
(1)求袋中白球的个数;
(2)第一次摸出一个球,做好记录后放回袋中,第二次再摸出一个球,请用列表或画树状图的方法求两次都摸到黄球的概率.
已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是
| A.0 | B.1 | C.2 | D.-2 |
张华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,同时与他邻近的
一棵树的影长为6米,则这棵树的高为
| A.3.2米 | B.4.8米 | C.5.2米 | D.5.6米 |
反比例函数y= (k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直
(k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直
x轴于点P,如果△MOP的面积为1,那么k的值是
| A.1 | B.2 | C.4 | D. |
下列四个命题中,假命题的是.
| A.有三个角是直角的四边形是矩形 |
| B.对角线互相垂直平分且相等的四边形是正方形 |
| C.四条边都相等的四边形是菱形 |
| D.顺次连接一个四边形各边中点,得到一个菱形,那么这个四边形是等腰梯形. |
函数y=(2m-1)x是正比例函数,且y随自变量x的增大而增大,则m的取值范围是
A.m> |
B.m< |
C.m≥ |
D.m≤ |
下列关于反比例函数的叙述,不正确的是
A.反比例函数y= 的图象绕原点旋转180°后,能与原来的图象重合; 的图象绕原点旋转180°后,能与原来的图象重合; |
B.反比例函数y= 的图象既不与x轴相交,也不与y轴相交; 的图象既不与x轴相交,也不与y轴相交; |
C.经过反比例函数y= 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于 ; ; |
D.反比例函数y= ,当k>0时,y随x的增大而减少。 ,当k>0时,y随x的增大而减少。 |
如图, 等腰梯形两底之差等于一腰的长,那么这个梯形较小内角的度数是
A. |
B. |
C. |
D. |
如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是
| A.S1> S2 | B. S1 = S2 |
| C. S1< S2 | D. S1、S2的大小关系不确定 |
如下左图,已知正方形ABCD的边长为m,△BPC是等边三角形,则△CDP的
面积为___ (用含m的代数式表示) .
如下右图,某同学从A点出发前进10米,向右转18°,再前进10米,又向右
转18°,这样下去,他第一次回到出发点A时,一共走了___________米.
已知:直角三角形的两边长分别是6和8,那么这个直角三角形的另一条边的长
是___________。
(本小题满分8分)如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形OCED是矩形吗?证明你的结论。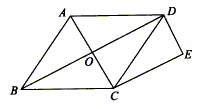
(本小题满分8分) 已知下列n(n为正整数)个关于x的一元二次方程:
①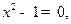 ②
② ③
③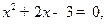
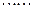 (n)
(n)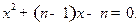
⑴请解上述一元二次方程①、②、③、(n);
⑵请你指出这n 个方程的根具有什么共同特点,写出一条即可。
(本小题满分10分)如图,小丽的家住在世通华庭的电梯公寓AD内,她家的对面新建了一座大厦BC。为了测得大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为60º,爬上楼顶D处测得大厦的顶部B的仰角为30º。已知小丽所住的电梯公寓高82米,请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。
(计算结果保留根号)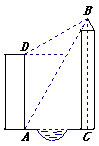
(本小题满分12分)你还记得图形的旋转吗?如图,P是正方形ABCD内一点,
PA=a,PB=2a,PC=3a.将△APB绕点B按顺时针方向旋转,使AB与BC重合,得△CBP,.
⑴ 求证:△PBP,是等腰直角三角形;
⑵ 猜想△PCP,的形状,并说明理由.
(本小题满分12分)已知反比例函数 和一次函数
和一次函数 ,其中一次
,其中一次
函数图象经过(a,b)与(a+1,b+k)两点.
(1) 求反比例函数的解析式.
(2) 如图,已知点A是第一象限内上述两个函数图象的交点,求A点坐标.
(3) 利用(2)的结果,请问:在X轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
 的倒数是( ).
的倒数是( ).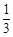
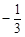
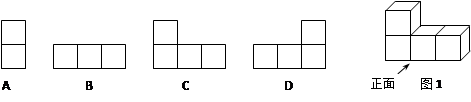
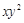 是同类项的是( ).
是同类项的是( ). 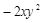
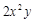
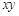
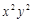
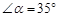 ,则
,则 的余角是 ( ).
的余角是 ( ).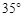

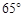
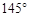
 的解集是( ).
的解集是( ). 
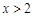
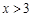
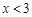
 、
、 、
、 在⊙O上,若
在⊙O上,若 ,则
,则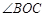 的度数为 ( ).
的度数为 ( ).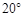
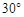
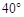
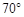

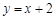 的图象大致是( ).
的图象大致是( ).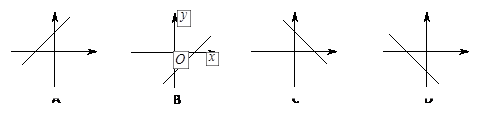
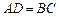
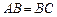
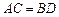
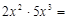 .
.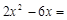 .
.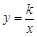 的图象经过点P(
的图象经过点P(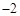 ,3),则
,3),则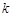 的值为 .
的值为 .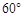 ,半径为6,则扇形的弧长为 .(结果保留
,半径为6,则扇形的弧长为 .(结果保留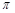 )
)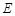 是
是 的中点,
的中点, 、
、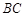 的延长线交于点
的延长线交于点 .若△
.若△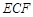 的面积为1,则四边形
的面积为1,则四边形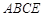 的面积为 .
的面积为 .
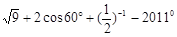 .
.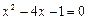 .
.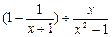 ,其中
,其中 .
.
 和
和 的图象大致是
的图象大致是 
 的图象经过A(-3,0)和B(O,2)两点,则
的图象经过A(-3,0)和B(O,2)两点,则 >0的解集是 .
>0的解集是 .
 的两个根,则这个三角形的周
的两个根,则这个三角形的周 经过点(-1,3),如果A(
经过点(-1,3),如果A( ),B(
),B( )两点在该双曲
)两点在该双曲 <
< <0,那么
<0,那么
 .
.
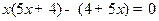
 是y关于x的反比例函数,且图
是y关于x的反比例函数,且图
 粤公网安备 44130202000953号
粤公网安备 44130202000953号