2011届广东省深圳市宝安区九年级第三次调研测试数学
(第1小题满分4分,第2小题满分5分,本题满分共9分)
(1)已知 ,从
,从 这4个数中任意选取3个数求和;
这4个数中任意选取3个数求和;
(2) ,试说明在右边代数式有意义的条件下,不论
,试说明在右边代数式有意义的条件下,不论 为
为
何值, 的值不变.
的值不变.
七年级十班为了表彰参加秋季运动会的队员,班主任特安排班长宋乐去商店买奖品,下面是宋乐与售货员的对话:
宋乐:阿姨,您好!
售货员:同学,你好,想买点什么?
宋乐:我只有100元,请帮我安排买10支钢笔和15本笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
为了进一步了解某校九年级学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
请结合图表完成下列问题:
(1)求表中 的值;
的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内 跳绳次数少于120次的为测试不合格,则该校九年级(1)班学生进行一分钟跳绳不合格的概率是多少?
跳绳次数少于120次的为测试不合格,则该校九年级(1)班学生进行一分钟跳绳不合格的概率是多少?
(本题满分8分)
如图,E、F分别是平行四边形ABCD对角线BD所在直线上两点,BE=DF,请你以F为一个端点,和图中己标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只需研究一组线段相等即可)
(1)连结_________
(2)猜想:_________
(3)证明:
(本题满分10分)
如图,已知正比例函数y = ax(a≠0)的图象与反比例函致 (k≠0)的图象的一个
(k≠0)的图象的一个
交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
(1)写出反比例函数和正比例函数的解析式;
(2)试计算△COE的面积是△ODE面积的多少倍.
(本题满分10分)
如图所示,在直角坐标系中,平行四边形OABC的顶点坐标B(6,3),C(2,3).
(1)求出过O、A、B三点的抛物线解析式;
(2)若直线 恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
(3)若 与
与 轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
线及 轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
已知 ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( )
| A.a<b<c | B.b<a<c | C.c<b<a | D.c<a<b |
在一次中学生科技制作展示赛上,蕲春县代表队一位模型赛车手遥控一辆赛车,先前进一米,然后原地逆时针方向旋转 °(0<
°(0< <180),被称为一次操作,若5次操作后回到出发点,则
<180),被称为一次操作,若5次操作后回到出发点,则 为( )。
为( )。
| A.72 | B.108或144 | C.144 | D.72或144 |
已知一次函数 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
| A.0 | B.1 | C.2 | D.大于2的整数 |
如图,圆的半径等于正△ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言, 的度数( )
的度数( )
A、保持30°不变, B、保持60°不变
C、从30°到60°变动 D、从60°到90°变动
设X、y定义为 ,X*2定义为X*2=
,X*2定义为X*2= ,则多项式
,则多项式 ( X*2)
( X*2) 在x=2时的值为( ).
在x=2时的值为( ).
| A.19 | B.27 | C.32 | D.38 |
如果a、b、c、d为互不相等的有理数,且|a-c|=|b-c|=|d-b|=1,则|a-b|=_______.
如图,∠AOB=45°,在∠AOB内点P处有一匹马,PO=2千米,牧马人从P处把马牵到河0A上的一点Q处饮马,再把马牵到草地OB上一点R处吃草,然后再回到P处,则该牧马人可走的最短路程为________千米。
南征中学2010年春季评出两名“孝星”(甲和乙),学校决定把7本不同的书奖给甲、乙两“孝星”,甲至少要分到2本,乙至少要分到1本,两人的本数不能只相差1,则不同的分法共有___________种。
2010广州亚运会田径场上有A、B、C、D、E、F六人参加百米决赛,对于谁是冠军,看台上甲、乙、丙、丁四人有以下猜测:
甲说:冠军不是A就是B。 乙说:冠军不是C。 丙说:D、E、F都不可能是冠军。丁说:冠军是D、E、F中的一人。比赛结果是,这四人只有一人的猜测是正确的,由此你判断冠军是___________。
。下表显示了去年夏天“蕲阳杯”钓鱼比赛的部分结果,这个表记录 了钓n条鱼的选手有多少名,n取不同的数值。
了钓n条鱼的选手有多少名,n取不同的数值。
在蕲春新闻中报道了如下信息:
| n |
0 |
1 |
2 |
3 |
…… |
13 |
14 |
15 |
| 钓到n条鱼的选手数 |
9 |
5 |
7 |
23 |
…… |
5 |
2 |
1 |
①钓钓鱼冠军钓到15条鱼;
②钓到3条或更多条鱼 的那些选手每人平均钓到6条鱼。
的那些选手每人平均钓到6条鱼。
③钓至12条或更少条鱼的那些选手每人平均钓到5条鱼。
由以上信息,求整个比赛中共钓到了多少条鱼?
(本 题满分10分),如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF=
题满分10分),如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF= (AB+AC)。
(AB+AC)。
,黄冈商城有甲、乙两汽车零售商向某品牌汽车生产厂订购一批汽车,甲开始订购的汽车数量是乙所订购数量的3倍,后来由于某种原因,甲从其所订的汽车中转让给乙6辆,在提车时,生产厂所提供的汽车比甲、乙所订购的总数少6辆,最后甲所购汽车的数量是乙所购的2倍,试问,甲、乙最后所购得的汽车总数最多是多少辆?最少又是多少辆?
,观察按下列规则排成的一列数:
(1)在这列数中,从左起第m个数记为F(m), 时,求m的值和这m个数的积。
时,求m的值和这m个数的积。
(2)在这列数中,未经约分且分母为2的数记为C,它后面的一个数记为d,是否存在这样的两个数c和d,使cd=2001000,如果存在,求出c和d;如果不存在,请说明理由。
2011年8月12日,第26届世界大学生夏季运动会将在深圳开幕。本届大运会的开幕式举办场地和主要分会场深圳湾体育中心总建筑面积达256520m2。数据256520m2用科学记数法(保留三个有效数字)表示为
A.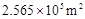 |
B.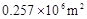 |
C.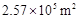 |
D.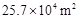 |
下列说法正确的是
A.一个游戏的中奖概率是 ,则做5次这样的游戏一定会中奖. ,则做5次这样的游戏一定会中奖. |
| B.为了解深圳中学生的心理健康情况,应该采用普查的方式. |
| C.事件“小明今年中考数学考95分”是可能事件. |
D.若甲组数据的方差 ,乙组数据的方差 ,乙组数据的方差 ,则乙组数据更稳定. ,则乙组数据更稳定. |
一个几何体由若干个小立方块搭成,它的主视图、左视图和俯视图分别如下,则搭出这个几何体的小立方块的个数是
| A.4个 | B.5个 |
| C.6个 | D.7个 |
如图1,已知函数 与函数
与函数 的图象交于A、B两点,过点A作
的图象交于A、B两点,过点A作
AC⊥y轴于C,过点B作BD⊥y轴于D,连接AD、BC.若四边形ACBD的面积是4,则 的值是
的值是 
A.8 B.4 C.2 D.1
矩形的周长是8,设一边长为x,另一边长为y,则下列图象中表示y与x之间的函数关系最恰当的是
A. B. C. D.
一家商店把某种“大运”纪念品按成本价提高50%后标价,又以8折(即按标价的80%优惠售出,结果每件仍获利2.4元,则这种纪念品的成本是
| A.3元 | B.4.8元 | C.6元 | D.12元 |
如图,Rt△ABC中,∠C=90º,∠A =30º,AB = 4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是

A. B.
B. C.
C. D.
D.
如图3,一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得此时影子DE的一端E到路灯A的仰角为45º,已知小颖的身高为1.5米,那么路灯A的高度AB为

| A.3米 | B.4.5米 | C.6米 | D.8米 |
如图4,菱形ABCD的对角线长分别为 ,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,……,如此下去,得到四边形A2011B2011C2011D2011的面积用含
,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,……,如此下去,得到四边形A2011B2011C2011D2011的面积用含 的代数式表示为
的代数式表示为
A. |
B. |
C. |
D. |
如图5,电路图上有三个开关A、B、C和一个小灯泡,当电路是通路时都可使灯泡发光。任意闭合其中两个开关,则小灯泡发光的概率等于__________
对于三个数 ,用
,用 表示这三个数的平均数,用
表示这三个数的平均数,用 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: ;
; ;
; .如果
.如果 ,则
,则 的值是______
的值是______
如图6,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=__________
如图7,菱形ABCD中,E是对角线AC上一点.

(1)求证:△ABE≌△ADE;
(2)若AB=AE,∠BAE=36º,求∠CDE的度数.
自从深圳获得第26届世界大学生运动会申办权以来,大运知识在我市不断传播。我市某中学举办大运知识测试,每班均随机抽出5位学生参加本次测试。张老师把所有参与测试的学生的成绩收集后,绘制出如下两幅不完整的统计图。

请你根据图中提供的信息解答以下问题:
(1)图8-1的统计图中,“九年级”所在的扇形的圆心角的度数是_________;
(2)如果九年级此次测试的总平均分是8.5分(满分是10分),请把图8-2的统计图补充完整;
(3)参加本次测试的学生共有______________人;
(4)如果此次测试的平均成绩是8分,那么这个成绩是否可用来估计我市中学生大运知识的平均水平?为什么?
某校组织九年级师生共270人参观市文博会,若单独租用甲种客车,则刚好坐满;若单独租用乙种客车,则可以少租一辆,且余30个空座位.已知每辆乙种客车比甲种客车多15个座位.
(1)求甲、乙两种客车每辆的座位分别有多少个;
(2)该校决定这次参观活动同时租用这两种车,其中乙种客车比甲种客车多租1辆,这样要比单独租用一种车辆节省租金.已知甲种客车的租金为每辆250元,乙种客车的租金为每辆300元,请你帮助计算本次参观活动所需车辆的租金.
如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长 线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;
(2)若PD是⊙O的切线,求x的值.
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.



 个图形比第
个图形比第 个图形多 枚
个图形多 枚
 的直径
的直径 的长为2
的长为2 ,
, 在
在 的延长线上,且
的延长线上,且 .
.
 的度数;
的度数; 是
是 ,其中
,其中 是弧长,
是弧长, 是半径,
是半径, 是圆心角度数)
是圆心角度数) 的两个根,b、c是方程
的两个根,b、c是方程 的两个根,则m=______
的两个根,则m=______ 的相反数是
的相反数是
 B
B  C
C D
D
 的结果是( )
的结果是( )



 _________
_________


 与x轴交于A、B两点,与y轴交于
与x轴交于A、B两点,与y轴交于

 粤公网安备 44130202000953号
粤公网安备 44130202000953号