(本题满分10分)
如图所示,在直角坐标系中,平行四边形OABC的顶点坐标B(6,3),C(2,3).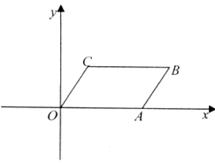
(1)求出过O、A、B三点的抛物线解析式;
(2)若直线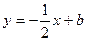 恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
(3)若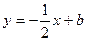 与
与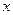 轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
线及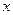 轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
相关知识点
推荐套卷
(本题满分10分)
如图所示,在直角坐标系中,平行四边形OABC的顶点坐标B(6,3),C(2,3).
(1)求出过O、A、B三点的抛物线解析式;
(2)若直线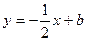 恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
(3)若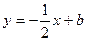 与
与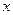 轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
线及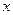 轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?
轴的交点分别记作点D、点E,试判断△OMN与△OED是否相似?