2011年初中毕业升学考试(宁夏卷)数学解析版
如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
(1)求证:△BDQ≌△ADP;
(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).
如图,已知抛物线y=﹣x2+bx+9﹣b2(b为常数)经过坐标原点O,且与x轴交于另一点E.其顶点M在第一象限.
(1)求该抛物线所对应的函数关系式;
(2)设点A是该抛物线上位于x轴上方,且在其对称轴左侧的一个动点;过点A作x轴的平行线交该抛物线于另一点D,再作AB⊥x轴于点B.DE⊥x轴于点C.
①当线段AB、BC的长都是整数个单位长度时,求矩形ABCD的周长;
②求矩形ABCD的周长的最大值,并写出此时点A的坐标;
③当矩形ABCD的周长取得最大值时,它的面积是否也同时取得最大值?请判断井说明理由.
为了了解某校七年级学生的身高情况从中抽取了200名学生,那么这次调查的总
体是_________________,个体是________________,样本容量是__________.
为了了解某校700名七年级新生入学时的数学水平,随机抽取若干名学生的数学成绩统计整理后绘制如图的频数分布直方图(分数取整数),观察图形回答下列问题:
(1)79~89的频数是______________. (2分)
(2)本次随机抽查的学生人数是多少人. (2分)
(3)被抽取的人数中有多少人不格. (2分)
(4)你能否估计一下700名七年级学生成绩不有格的有多少人? (2分)
七年级(3)班在召开期末总结表彰会之前,班主任安排班长去商店买奖品,下面是班长与售货员的对话.
班长:阿姨,您好!
售货员:同学,你好!想买点什么吗?
班长:我只有100元,请帮我安排买10枝钢笔和15本笔记本.
售货员:好的,每枝钢笔比每本笔记本贵2元,退你5元,请点好,再见!
根据这段对话,你能算出钢笔和笔记本的单价各是多少元吗? (8分)
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AB的长是( )
| A.2 | B.4 |
C.2 |
D.4 |
等腰梯形的上底是2cm,腰长是4cm,一个底角是60°,则等腰梯形的下底是( )
| A.5cm | B.6cm |
| C.7cm | D.8cm |
一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,所列方程组正确的是( )
A.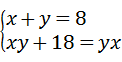 |
B.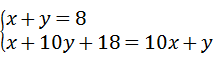 |
C.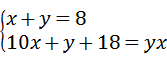 |
D.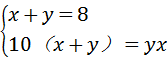 |
将“创建文明城市”六个字分别写在一个正方体的六个面上,这 个正方体的平面展开图如图所示,那么在这个正方体中,和“创“相对的字是( )
个正方体的平面展开图如图所示,那么在这个正方体中,和“创“相对的字是( )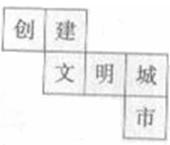
| A.文 | B.明 |
| C.城 | D.市 |
已知⊙O1、⊙O2的半径分别是r1=3、r2=5.若两圆相切,则圆心距O1O2的值是( )
| A.2或4 | B.6或8 |
| C.2或8 | D.4或6 |
某校A、B两队10名参加篮球比赛的队员的身高(单位:cm)如下表所示:
| 队员 队 |
1号 |
2号 |
3号 |
4号 |
5号 |
| A队 |
176 |
175 |
174 |
171 |
174 |
| B队 |
170 |
173 |
171 |
174 |
182 |
设两队队员身高的平均数分别为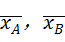 ,身高的方差分别为SA2,SB2,则正确的选项是( )
,身高的方差分别为SA2,SB2,则正确的选项是( )
A、 B、
B、
C、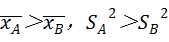 D、
D、
如图,△ABO的顶点坐标分别为A(1,4)、B(2,1)、O(0,0),如果将△ABO绕点O按逆时针方向旋转90°,得到△A′B′O′,那么点A′、B′的对应点的坐标是( )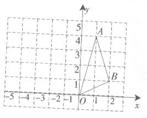
| A.A′(﹣4,2),B′(﹣1,1) | B.A′(﹣4,1),B′(﹣1,2) |
| C.A′(﹣4,1),B′(﹣1,1) | D.A′(﹣4,2),B′(﹣1,2) |
若线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C(3,6),则点B(﹣5,﹣2)的对应点D的坐标是 .
在一次社会实践活动中,某班可筹集到的活动经费最多900元.此次活动租车需300元,每个学生活动期间所需经费15元,则参加这次活动的学生人数最多为 .
有一个均匀的正六面体,六个面上分别标有数字1,2,3,4,5,6,随机地抛掷一次,把朝上一面的数字记为x;另有三张背面完 全相同,正面分布写有数字﹣2,﹣1,1的卡片,将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后计算出S=x+y的值.
全相同,正面分布写有数字﹣2,﹣1,1的卡片,将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后计算出S=x+y的值.
(1)用树状图或列表法表示出S的所有可能情况;
(2)求出当S<2时的概率.
我市某中学九年级学生对市民“创建精神文明城市“知 晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
| 等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
从未听说 |
| 频数 |
40 |
60 |
48 |
36 |
16 |
| 频率 |
0.2 |
m |
0.24 |
0.18 |
0.08 |
(1)本次问卷调查抽取的样本容量为 ,表中m的值为 ;
(2)根据表中的数据计算等级为“非常广解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.
已知,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF.求证:四边形A BCD是平行四边形.
已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.
(1)求证:PD是⊙O的切线;
(2)若∠CAB=120°,AB= 2,求BC的值.
2,求BC的值.
在Rt△ABC中,∠C=90°,∠A=30°,BC=2.若将此直角三角形的一条直角边BC或AC与x轴重合,使点A或点B刚好在反比例函数 (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示) D是斜边与y轴的交点,通过计算比较S1、S2的大小.
D是斜边与y轴的交点,通过计算比较S1、S2的大小.
甲、乙两人分别乘不同的冲锋舟同时从A地逆流而上前往B地.甲所乘冲锋舟在静水中的速度为 千米/分钟,甲到达B地立即返回.乙所乘冲锋舟在在静水中的速度
千米/分钟,甲到达B地立即返回.乙所乘冲锋舟在在静水中的速度 为
为 千米/分钟.已知A、B两地的距离为20千米,水流速度为
千米/分钟.已知A、B两地的距离为20千米,水流速度为 千米/分钟,甲、乙乘冲锋舟行驶的距离y(千米)与所用时间x(分钟)之间的函数图象如图所示.
千米/分钟,甲、乙乘冲锋舟行驶的距离y(千米)与所用时间x(分钟)之间的函数图象如图所示.
(1)求甲所乘冲锋舟在行驶的整个过程中,y与x之间的函数关系式.
(2)甲、乙两人同时出发后,经过多少分钟相遇?.
 的解集为( )
的解集为( ) ,则
,则 的度数为( )
的度数为( )



 中是二元一次方程的有( )个.
中是二元一次方程的有( )个. ( )
( )
 的解集是( )
的解集是( )
 ,则图中表示正确的是( )
,则图中表示正确的是( )
 ,则下列长度的线段能作为第三边的是( )
,则下列长度的线段能作为第三边的是( ) 的正整数解有( )个
的正整数解有( )个 的解是________________.
的解是________________.


 三个顶点的坐标.
三个顶点的坐标. .
.
 .求
.求
 的度数.(8分)
的度数.(8分)
 ( )
( ) 和2,若点A关于点B的对称点为点C,则点C所对应的实数为 .
和2,若点A关于点B的对称点为点C,则点C所对应的实数为 .

 )﹣2﹣|
)﹣2﹣| ﹣2|
﹣2| .
. .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号