初中数学圆解答题

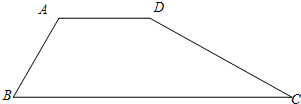
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE。已知∠BAC=30º，EF⊥AB，垂足为F，连结DF。
（1）试说明AC=EF；
（2）求证：四边形ADFE是平行四边形。

(8分)如图，将直角三角形纸片ABC沿边BC所在直线向右平移，使B点移至斜
边BC的中点E处，连接AD、AE、CD。
（1）求证：四边形AECD是菱形。
（2）若直角三角形纸片ABC的斜边BC的长为100cm，且AC＝60cm.求ED的长 和四边形AECD的面积；

如图，矩形中，与交于点，⊥，⊥，垂足分别为，．试比较．BE与CF的大小，并说明理由

如图，在梯形ABCD中，AD∥BC，AC、BD是对角线．过点D作DE
∥AC，交BC的延长线于点E．
（1）判断四边形ACED的形状并证明；
（2）若AC＝DB，求证：梯形ABCD是等腰梯形．

如图，在四边形ABCD中，AD//BC，E、F为AB上两点，且△DAF
≌△CBE．

求证：（1）∠A＝90°；
（2）四边形ABCD是矩形．

(9分)如图(1)，正方形ABCD中，点H从点C出发，沿CB运动到点B停止．连
结DH交正方形对角线AC于点E，过点E作DH的垂线交线段AB、CD于点F、G．
（1）求证： DH＝FG；
（2）在图(1)中延长FG与BC交于点P，连结DF、DP（如图（2）），试探究DF与DP的关系，并说明理由．

. (7分)已知：如图，□ABCD中，∠BCD的平分线交AB于E，交DA的延长线于F．
(1) 求证：DF＝DC；
(2) 当DE⊥FC时，求证：AE＝BE．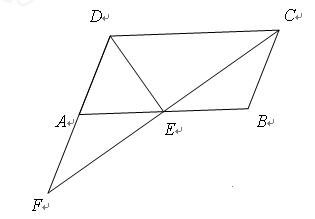

如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，AE∥BC, DE∥AB.

证明：（1）AE=DC；
（2）四边形ADCE为矩形．

已知：如图，直角梯形中，，
，求的长．

已知，如图，梯形ABCD中，AD∥BC,∠A=90°，∠C=45°，BE⊥DC于E，BC=5，AD:BC=2:5.求ED的长.

（1）如图①两个正方形的边长均为3，求三角形DBF的面积.
（2）如图②，正方形ABCD的边长为3，正方形CEFG的边长为1, 求三角形DBF的面积.
（3）如图③，正方形ABCD的边长为a，正方形CEFG的边长为，求三角形DBF的面积.

从上面计算中你能得到什么结论.
结论是：
（没写结论也不扣分）

已知:如图，在四边形ABFC中，=90°,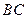的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
（1）求证：四边形BECF是菱形；
（2）当的大小为多少度时,四边形BECF是正方形？

（本小题满分5分）如图，A、B、C三点在同一条直线上，AB=2BC，分别以AB，BC为边做正方形ABEF和正方形BCMN，联结FN，EC． 求证：FN=EC

如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．
（1）求证：AD=AE；
（2）若AD=8，DC=4，求AB的长．

已知梯形ABCD中，AD∥BC，AB=AD（如图所示），∠BAD的平分线AE交BC于点E，连接DE．
（1）在下图中，用尺规作∠BAD的平分线AE（保留作图痕迹不写作法），并证明四边形ABED是菱形．
（2）若∠ABC=60°，EC=2BE．求证：ED⊥DC．